What is scaled scoring on a test?
Scaled scoring is a process used in assessment and psychometrics to transform exam scores to another scale (set of numbers), typically to make the scores more easily interpretable but also to hide sensitive information like raw scores and differences in form difficulty (equating). For example, the ACT test produces scores on a 0 to 36 scale; obviously, there are more than 36 questions on the test, so this is not your number correct score, but rather a repackaging. So how does this repackaging happen, and why are we doing it in the first place?
An Example of Scales: Temperature
First, let’s talk about the definition of a scale. A scale is a range of numbers for which you can assign values and interpretations. Scores on a student essay might be 0 to 5 points, for example, where 0 is horrible and 5 is wonderful. Raw scores on a test, like number-correct, are also a scale, but there are reasons to hide this, which we will discuss.
An example of scaling that we are all familiar with is temperature. There are three scales that you have probably heard of: Fahrenheit, Celsius, and Kelvin. Of course, the concept of temperature does not change, we are just changing the set of numbers used to report it. Water freezes at 32 Fahrenheit and boils at 212, while these numbers are 0 and 100 with Celsius. Same with assessment: the concept of what we are measuring does not change on a given exam (e.g., knowledge of 5th grade math curriculum in the USA, mastery of Microsoft Excel, clinical skills as a neurologist), but we can change the numbers.
What is Scaled Scoring?
In assessment and psychometrics, we can change the number range (scale) used to report scores, just like we can change the number range for temperature. If a test is 100 items but we don’t want to report the actual score to students, we can shift the scale to something like 40 to 90. Or 0 to 5. Or 824,524 to 965,844. It doesn’t matter from a mathematical perspective. But since one goal is to make it more easily interpretable for students, the first two are much better than the third.
So, if an organization is reporting Scaled Scores, it means that they have picked some arbitrary new scale and are converting all scores to that scale. Here’s some examples…
Real Examples
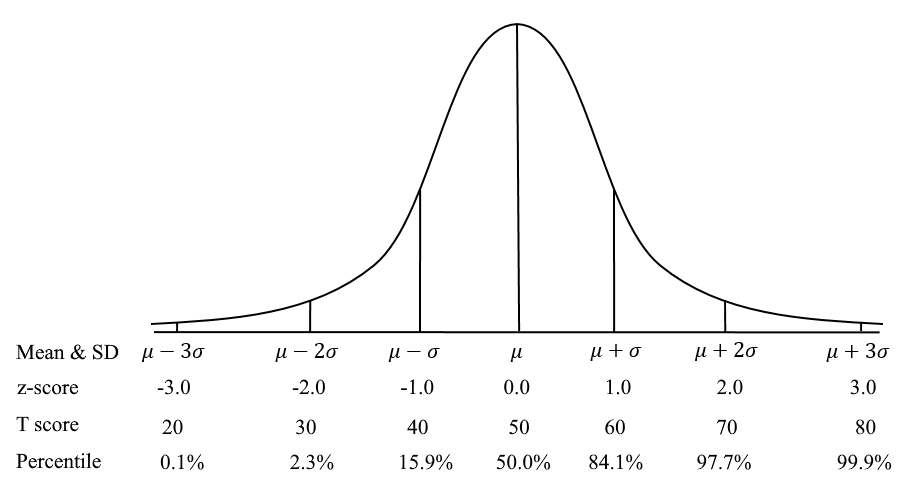
Many assessments are normed on a standard normal bell curve. Those which use item response theory do so implicitly, because scores are calculated directly on the z-score scale (there are some semantic differences, but it’s the basic idea). Well, any scores on the z-score bell curve can be converted to other scales quite easily, and back again. Here some of the common scales used in the world of assessment.
| z score | T score | IQ | Percentile | ACT | SAT |
| -3 | 20 | 55 | 0.02 | 0 | 200 |
| -2 | 30 | 70 | 2.3 | 6 | 300 |
| -1 | 40 | 85 | 15.9 | 12 | 400 |
| 0 | 50 | 100 | 50 | 18 | 500 |
| 1 | 60 | 115 | 84.1 | 24 | 600 |
| 2 | 70 | 130 | 97.7 | 30 | 700 |
| 3 | 80 | 145 | 99.8 | 36 | 800 |
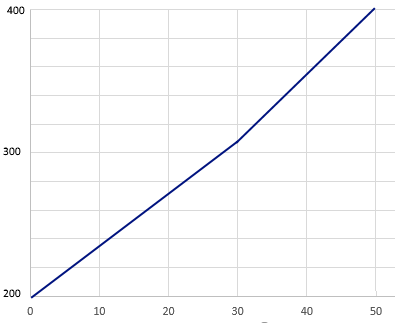
Note how the translation from normal curve based approaches to Percentile is very non-linear! The curve-based approaches stretch out the ends. Here is how these numbers look graphically.
Why do Scaled Scoring?
There are a few good reasons:
- Differences in form difficulty (equating) – Many exams use multiple forms, especially across years. What if this year’s form has a few more easy questions and we need to drop the passing score by 1 point on the raw score metric? Well, if you are using scaled scores like 200 to 400 with a cutscore of 350, then you just adjust the scaling each year so the reported cutscore is always 350.
- Hiding the raw score – In many cases, even if there is only one form of 100 items, you don’t want students to know their actual score.
- Hiding the z scale (IRT) – IRT scores people on the z-score scale. Nobody wants to be told they have a score of -2. That makes it feel like you have negative intelligence or something like that. But if you convert it to a big scale like the SAT above, that person gets a score of 300, which is a big number so they don’t feel as bad. This doesn’t change the fact that they are only at the 2nd percentile though. It’s just public relations and marketing, really.
Who uses Scaled Scoring?
Just about all the “real” exams in the world use this. Of course, most use IRT, which makes it even more important to use scaled scoring.
Methods of Scaled Scoring
There are 4 types of scaled scoring. The rest of this post will get into some psychometric details on these, for advanced readers.
- Normal/standardized
- Linear
- Linear dogleg
- Equipercentile
Normal/standardized
This is an approach to scaled scoring that many of us are familiar with due to some famous applications, including the T score, IQ, and large-scale assessments like the SAT. It starts by finding the mean and standard deviation of raw scores on a test, then converts whatever that is to another mean and standard deviation. If this seems fairly arbitrary and doesn’t change the meaning… you are totally right!
Let’s start by assuming we have a test of 50 items, and our data has a raw score average of 35 points with an SD of 5. The T score transformation – which has been around so long that a quick Googling can’t find me the actual citation – says to convert this to a mean of 50 with an SD of 10. So, 35 raw points become a scaled score of 50. A raw score of 45 (2 SDs above mean) becomes a T of 70. We could also place this on the IQ scale (mean=100, SD=15) or the classic SAT scale (mean=500, SD=100).
A side not about the boundaries of these scales: one of the first things you learn in any stats class is that plus/minus 3 SDs contains 99% of the population, so many scaled scores adopt these and convenient boundaries. This is why the classic SAT scale went from 200 to 800, with the urban legend that “you get 200 points for putting your name on the paper.” Similarly, the ACT goes from 0 to 36 because it nominally had a mean=18 and SD=6.
The normal/standardized approach can be used with classical number-correct scoring, but makes more sense if you are using item response theory, because all scores default to a standardized metric.
Linear
The linear approach is quite simple. It employs the y=mx+b that we all learned as schoolkids. With the previous example of a 50 item test, we might say intercept=200 and slope=4. This then means that scores range from 200 to 400 on the test.
Yes, I know… the Normal conversion above is technically linear also, but deserves its own definition.
Linear dogleg
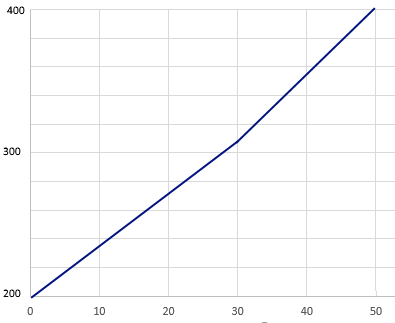
The Linear Dogleg approach is a special case of the previous one, where you need to stretch the scale to reach two endpoints. Let’s suppose we published a new form of the test, and a classical equating method like Tucker or Levine says that it is 2 points easier and the slope of Form A to Form B is 3.8 rather than 4. This throws off our clean conversion of 200 to 400 scale. So suppose we use the equation SCALED = 200 + 3.8*RAW but only up until the score of 30. From 31 onwards, we use SCALED = 185 + 4.3*RAW. Note that the raw score of 50 then still comes out to be scaled of 400, so we still go from 200 to 800 but there is now a slight bend in the line. This is called the “dogleg” similar to the golf hole of the same name.
Equipercentile
Lastly, there is Equipercentile, which is mostly used for equating forms but can similarly be used for scaling. In this conversion, we match the percentile for each, even if it is a very nonlinear transformation. For example, suppose our Form A had a 90th percentile of 46, which became a scale of 384. We find that Form B has a 90th percentile at 44 points, so we call that a scaled score of 384, and calculate a similar conversion for all other points.
Why are we doing this again?
Well, you can kind of see it in the example of having two forms with a difference in difficulty. In the Equipercentile example, suppose there is a cut score to be in the top 10% to win a scholarship. If you get 45 on Form A you will lose, but if you get 45 on Form B you will win. Test sponsors don’t want to have this conversation with angry examinees, so they convert all scores to an arbitrary scale. The 90th percentile is always a 384, no matter how hard the test is. (Yes, that simple example assumes the populations are the same… there’s an entire portion of psychometric research dedicated to performing stronger equating.)
How do we implement scaled scoring?
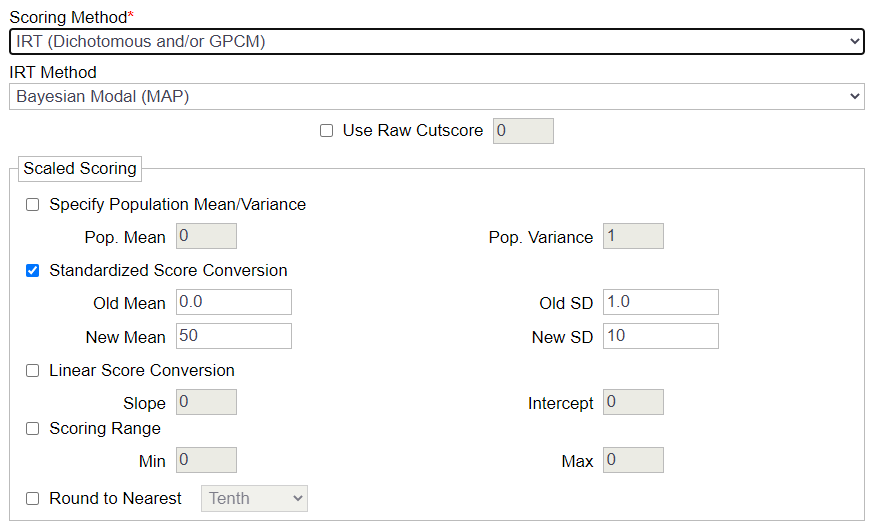
Some transformations are easily done in a spreadsheet, but any good online assessment platform should handle this topic for you. Here’s an example screenshot from our software.
Nathan Thompson, PhD
Latest posts by Nathan Thompson, PhD (see all)
- What is a T score? - April 15, 2024
- Item Review Workflow for Exam Development - April 8, 2024
- Likert Scale Items - February 9, 2024
