If you are delivering high-stakes tests in linear forms – or piloting a bank for CAT/LOFT – you are faced with the issue of how to equate the forms together. That is, how can we defensibly translate a score on Form A to a score on Form B? While the concept is simple, the methodology can be complex, and there is an entire area of psychometric research devoted to this topic. There are a number of ways to approach this issue, and IRT equating is the strongest.
Why do we need equating?
The need is obvious: to adjust for differences in difficulty to ensure that all examinees receive a fair score on a stable scale. Suppose you take Form A and get s score of 72/100 while your friend takes Form B and gets a score of 74/100. Is your friend smarter than you, or did his form happen to have easier questions? Well, if the test designers built-in some overlap, we can answer this question empirically.
Suppose the two forms overlap by 50 items, called anchor items or equator items. Both forms are each delivered to a large, representative sample. Here are the results.
Form
Mean score on 50 overlap items
Mean score on 100 total items
A
30
72
B
30
74
Because the mean score on the anchor items was higher, we then think that the Form B group was a little smarter, which led to a higher total score.
Now suppose these are the results:
Form
Mean score on 50 overlap items
Mean score on 100 total items
A
32
72
B
32
74
Now, we have evidence that the groups are of equal ability. The higher total score on Form B must then be because the unique items on that form are a bit easier.
How do I calculate an equating?
You can equate forms with classical test theory (CTT) or item response theory (IRT). However, one of the reasons that IRT was invented was that equating with CTT was very weak. CTT methods include Tucker, Levine, and equipercentile. Right now, though, let’s focus on IRT.
IRT equating
There are three general approaches to IRT equating. All of them can be accomplished with our industry-leading software Xcalibre, though conversion equating requires an additional software called IRTEQ.
Conversion
Concurrent Calibration
Fixed Anchor Calibration
Conversion
With this approach, you need to calibrate each form of your test using IRT, completely separately. We then evaluate the relationship between IRT parameters on each form and use that to estimate the relationship to convert examinee scores. Theoretically what you do is line up the IRT parameters of the common items and perform a linear regression, so you can then apply that linear conversion to scores.
But DO NOT just do a regular linear regression. There are specific methods you must use, including mean/mean, mean/sigma, Stocking & Lord, and Haebara. Fortunately, you don’t have to figure out all the calculations yourself, as there is free software available to do it for you: IRTEQ.
Concurrent Calibration
The second approach is to combine the datasets into what is known as a sparse matrix. You then run this single data set through the IRT calibration, and it will place all items and examinees onto a common scale. The concept of a sparse matrix is typically represented by the figure below, representing the non-equivalent anchor test (NEAT) design approach.
The IRT calibration software will automatically equate the two forms and you can use the resultant scores.
Fixed Anchor Calibration
The third approach is a combination of the two above; it utilizes the separate calibration concept but still uses the IRT calibration process to perform the equating rather than separate software.
With this approach, you would first calibrate your data for Form A. You then find all the IRT item parameters for the common items and input them into your IRT calibration software when you calibrate Form B.
You can tell the software to “fix” the item parameters so that those particular ones (from the common items) do not change. Then all the item parameters for the unique items are forced onto the scale of the common items, which of course is the underlying scale from Form A. This then also forces the scores from the Form B students onto the Form A scale.
How do these IRT equating approaches compare to each other?
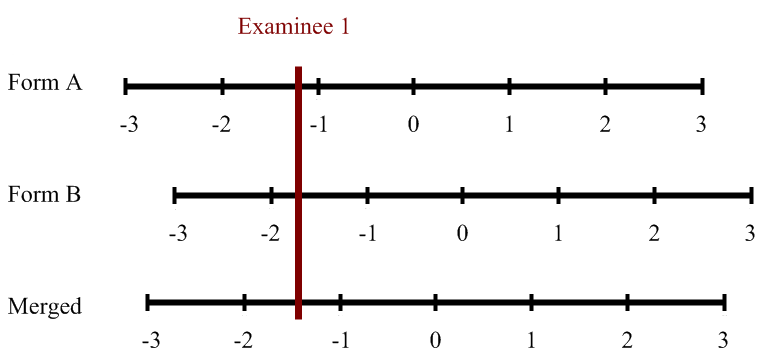
Concurrent calibration is arguably the easiest but has the drawback that it merges the scales of each form into a new scale somewhere in the middle. If you need to report the scores on either form on the original scale, then you must use the Conversion or Fixed Anchor approaches. This situation commonly happens if you are equating across time periods.
Suppose you delivered Form A last year and are now trying to equate Form B. You can’t just create a new scale and thereby nullify all the scores you reported last year. You must map Form B onto Form A so that this year’s scores are reported on last year’s scale and everyone’s scores will be consistent.
Where do I go from here?
If you want to do IRT equating, you need IRT calibration software. All three approaches use it. I highly recommend Xcalibre since it is easy to use and automatically creates reports in Word for you. If you want to learn more about the topic of equating, the classic reference is the book by Kolen and Brennan (2004; 2014). There are other resources more readily available on the internet, like this free handbook from CCSSO. If you would like to learn more about IRT, I recommend the books by de Ayala (2008) and Embretson & Reise (2000). An intro is available in our blog post.
Nathan Thompson earned his PhD in Psychometrics from the University of Minnesota, with a focus on computerized adaptive testing. His undergraduate degree was from Luther College with a triple major of Mathematics, Psychology, and Latin. He is primarily interested in the use of AI and software automation to augment and replace the work done by psychometricians, which has provided extensive experience in software design and programming. Dr. Thompson has published over 100 journal articles and conference presentations, but his favorite remains https://pareonline.net/getvn.asp?v=16&n=1.
