What is the Sympson-Hetter Item Exposure Control?
Content
Sympson-Hetter is a method of item exposure control within the algorithm of Computerized adaptive testing (CAT). It prevents the algorithm from over-using the best items in the pool.
CAT is a powerful paradigm for delivering tests that are smarter, faster, and fairer than the traditional linear approach. However, CAT is not without its challenges. One is that it is a greedy algorithm that always selects your best items from the pool if it can. The way that CAT researchers address this issue is with item exposure controls. These are sub algorithms that are injected into the main item selection algorithm, to alter it from always using the best items. The Sympson-Hetter method is one such approach. Another is the Randomesque method.
The Randomesque Method
The simplest approach is called the randomesque method. This selects from the top X items in terms of item information (a term from item response theory), usually for the first Y items in a test. For example, instead of always selecting the top item, the algorithm finds the 3 top items and then randomly selects between those.
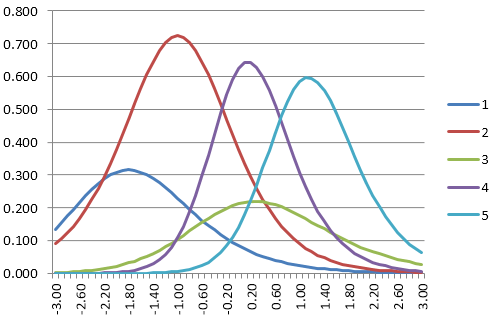
The figure on the right displays item information functions (IIFs) for a pool of 5 items. Suppose an examinee had a theta estimate of 1.40. The 3 items with the highest information are the light blue, purple, and green lines (5, 4, 3). The algorithm would first identify this and randomly pick amongst those three. Without item exposure controls, it would always select Item 4.
The Sympson-Hetter Method
A more sophisticated method is the Sympson-Hetter method.
Here, the user specifies a target proportion as a parameter for the selection algorithm. For example, we might decide that we do not want an item seen by more than 75% of examinees. So, every time that the CAT algorithm goes into the item pool to select a new item, we generate a random number between 0 and 1, which is then compared to the threshold. If the number is between 0 and 0.75 in this case, we go ahead and administer the item. If the number is from 0.75 to 1.0, we skip over it and go on to the next most informative item in the pool, though we then do the same comparison for that item.
Why do this? It obviously limits the exposure of the item. But just how much it limits it depends on the difficulty of the item. A very difficult item is likely only going to be a candidate for selection for very high-ability examinees. Let’s say it’s the top 4%… well, then the approach above will limit it to 3% of the sample overall, but 75% of the examinees in its neighborhood.
On the other hand, an item of middle difficulty is used not only for middle examinees but often for any examinee. Remember, unless there are some controls, the first item for the test will be the same for everyone! So if we apply the Sympson-Hetter rule to that item, it limits it to 75% exposure in a more absolute sense.
Because of this, you don’t have to set that threshold parameter to the same value for each item. The original recommendation was to do some CAT simulation studies, then set the parameters thoughtfully for different items. Items that are likely to be highly exposed (middle difficulty with high discrimination) might deserve a more strict parameter like 0.40. On the other hand, that super-difficult item isn’t an exposure concern because only the top 4% of students see it anyway… so we might leave its parameter at 1.0 and therefore not limit it at all.
Is this the only method available?
No. As mentioned, there’s that simple randomesque approach. But there are plenty more. You might be interested in this paper, this paper, or this paper. The last one reviews the research literature from 1983 to 2005.
What is the original reference?
Sympson, J. B., & Hetter, R. D. (1985, October). Controlling item-exposure rates in computerized adaptive testing. Proceedings of the 27th annual meeting of the Military Testing Association (pp. 973–977). San Diego, CA: Navy Personnel Research and Development Center.
How can I apply this to my tests?
Well, you certainly need a CAT platform first. Our platform at ASC allows this method right out of the box – that is, all you need to do is enter the target proportion when you publish your exam, and the Sympson-Hetter method will be implemented. No need to write any code yourself! Click here to sign up for a free account.
Nathan Thompson, PhD
Latest posts by Nathan Thompson, PhD (see all)
- Situational Judgment Tests: Higher Fidelity in Pre-Employment Testing - November 30, 2024
- What is an Assessment-Based Certificate? - October 12, 2024
- What is Psychometrics? How does it improve assessment? - October 12, 2024
