The Graded Response Model – Samejima (1969)
Content
Samejima’s (1969) Graded Response Model (GRM, sometimes SGRM) is an extension of the two parameter logistic model (2PL) within the item response theory (IRT) paradigm. IRT provides a number of benefits over classical test theory, especially regarding the treatment of polytomous items; learn more about IRT vs. CTT here.
What is the Graded Response Model?
GRM is a family of latent trait (latent trait is a variable that is not directly measurable, e.g. a person’s level of neurosis, conscientiousness or openness) mathematical models for grading responses that was developed by Fumiko Samejima in 1969 and has been utilized widely since then. GRM is also known as Ordered Categorical Responses Model as it deals with ordered polytomous categories that can relate to both constructed-response or selected-response items where examinees are supposed to obtain various levels of scores like 0-4 points. In this case, the categories are as follows: 0, 1, 2, 3, and 4; and they are ordered. ‘Ordered’ means what it says, that there is a specific order or ranking of responses. ‘Polytomous’ means that the responses are divided into more than two categories, i.e., not just correct/incorrect or true/false.
When should I use the GRM?
This family of models is applicable when polytomous responses to an item can be classified into more than two ordered categories (something more than correct/incorrect), such as to represent different degrees of achievement in a solution to a problem or levels of agreement , a Likert scale, or frequency to a certain statement. GRM covers both homogeneous and heterogeneous cases, while the former implies that a discriminating power underlying a thinking process is constant throughout a range of attitude or reasoning.
Samejima (1997) highlights a reasonability of employing GRM in testing occasions when examinees are scored based on correctness (e.g., incorrect, partially correct, correct) or while measuring people’s attitudes and preferences, like in Likert-scale attitude surveys (e.g., strongly agree, agree, neutral, disagree, strongly disagree). For instance, GRM can be used in an extroversion scoring model considering “I like to go to parties” as a high difficulty construction, and “I like to go out for coffee with a close friend” as an easy one.
Here are some examples of assessments where GRM is utilized:
- Survey attitude questions using responses like ‘strongly disagree, disagree, neutral, agree, strongly agree’
- Multiple response items, such as a list of 8 animals and student selects which 3 are reptiles
- Drag and drop or other tech enhanced items with multiple points available
- Letter grades assigned to an essay: A, B, C, D, and E
- Essay responses graded on a 0-to-4 rubric
Why to use GRM?
There are three general goals of applying GRM:
- estimating an ability level/latent trait
- estimating an adequacy with which test questions measure an ability level/latent trait
- evaluating a probability that a particular test domain will receive a specific score/grade for each question
Using item response theory in general (not just the GRM) provides a host of advantages. It can help you validate the assessment. Using the GRM can also enable adaptive testing.
How to calculate a response probability with the GRM?
There is a two-step process of calculating a probability that an examinee selects a certain category in a given question. The first step is to find a probability that an examinee with a definite ability level selects a category n or greater in a given question:
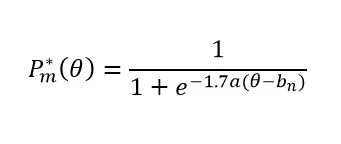
where
1.7 is the scale factor
a is the discrimination of the question
bm is a probability of choosing category n or higher
e is the constant that approximately equals to 2.718
Θ is the ability level
P*m(Θ) = 1 if m = 1 since a probability of replying in the lowest category or in all the major ones is a certain event
P*m(Θ) = 0 if m = M + 1 since a probability of replying in a category following the largest is null.
The second step is to find a probability that an examinee responds in a given category:
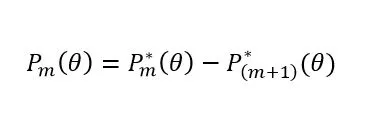
This formula describes the probability of choosing a specific response to the question for each level of the ability it measures.
How do I implement the GRM on my assessment?
You need item response theory software. Start by downloading Xcalibre for free. Below are outputs for two example items.
How to interpret this? The GRM uses category response functions which show the probability of selecting a given response as a function of theta (trait or ability). For item 6, we see that someone of theta -3.0 to -0.5 is very likely to select “2” on the Likert scale (or whatever our response is). Examinees above -.05 are likely to select “3” on the scale. But on Item 10, the green curve is low and not likely to be chosen at all; examinees from -2.0 to +2.0 are likely to select “3” on the Likert scale, and those above +2.0 are likely to select “4”. Item 6 is relatively difficult, in a sense, because no one chose “4.”
| Item 6 | Item 10 |
 |
 |
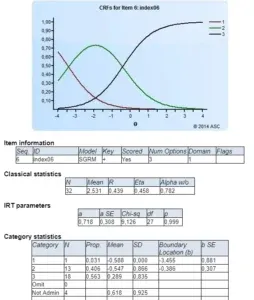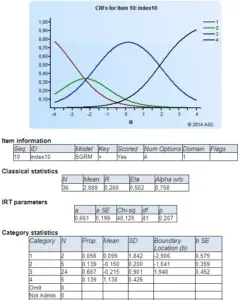References
Keller, L. A. (2014). Item Response Theory Models for Polytomous Response Data. Wiley StatsRef: Statistics Reference Online.
Samejima, F. (1969). Estimation of latent ability using a response pattern of graded coress. Psychometrika monograph supplement, 17(4), 2. doi:10.1002/j.2333-8504.1968.tb00153.x.
Samejima, F. (1997). Graded response model. In W. J. van der Linden and R. K. Hambleton (Eds), Handbook of Modern Item Response Theory, (pp. 85–100). Springer-Verlag.
Laila Issayeva M.Sc.
Latest posts by Laila Issayeva M.Sc. (see all)
- What is a z-score? - November 28, 2024
- Confidence Intervals in Assessment and Psychometrics - November 25, 2024
- General Intelligence and Its Role in Assessment and Measurement - November 10, 2024
