Harpp, Hogan, and Jennings (1996) revised their Response Similarity Index somewhat from Harpp and Hogan (1993). This produced a new equation for a statistic to detect collusion and other forms of exam cheating:.
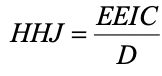
Explanation of Response Similarity Index
EEIC denote the number of exact errors in common or identically wrong,
D is the number of items with a different response.
Note that D is calculated across all items, not just incorrect responses, so it is possible (and likely) that D>EEIC. Therefore, the authors suggest utilizing a flag cutoff of 1.0 (Harpp, Hogan, & Jennings, 1996):
Analyses of well over 100 examinations during the past six years have shown that when this number is ~1.0 or higher, there is a powerful indication of cheating. In virtually all cases to date where the exam has ~30 or more questions, has a class average <80% and where the minimum number of EEIC is 6, this parameter has been nearly 100% accurate in finding highly suspicious pairs.
However, Nelson (2006) has evaluated this index in comparison to Wesolowsky’s (2000) index and strongly recommends against using the HHJ. It is notable that neither makes any attempt to evaluate probabilities or standardize. Cizek (1999) notes that both Harpp-Hogan methods do not even receive attention in the psychometric literature.
This approach has very limited ability to detect cheating when the source has a high ability level. While individual classroom instructors might find the EEIC/D straightforward and useful, there are much better indices for use in large-scale, high-stakes examinations.

Nathan Thompson earned his PhD in Psychometrics from the University of Minnesota, with a focus on computerized adaptive testing. His undergraduate degree was from Luther College with a triple major of Mathematics, Psychology, and Latin. He is primarily interested in the use of AI and software automation to augment and replace the work done by psychometricians, which has provided extensive experience in software design and programming. Dr. Thompson has published over 100 journal articles and conference presentations, but his favorite remains https://scholarworks.umass.edu/pare/vol16/iss1/1/ .
