Holland K

Holland K Index and K Variants for Forensics

Nathan Thompson, PhDJuly 25, 2020

The Holland K index and variants are probability-based indices for psychometric forensics, like the Bellezza & Bellezza indices, but make use of conditional information in their calculations. All three estimate the probability of observing  wij  or more identical incorrect responses (that is, EEIC, exact errors in common) between a pair of examinees in a directional fashion. This is defined as

Holland K.

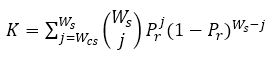Here, Ws is the number of items answered incorrectly by the source, Wcs is the EEIC, and Pr is the probability of the source and copier having the same incorrect response to an item.  So, if the source had 20 items incorrect and the suspected copier had the same answer for 18 of them, we are calculating the probability of having 18 EEIC (the right side), then multiplying it by the number of ways there can be 18 EEICs in a set of 20 items (the middle).  Finally, we do the same for 19 and 20 EEIC and sum up our three values.  In this example, that would likely be summing three very small values because Pr is being taken to large powers and it is a probability such as 0.4.  Such a situation would be very unlikely, so we’d expect a K index value of 0.000012.

If there were no cheating, the copier might have only 3 EEIC with the source, and we’d be summing from 3 up to 20, with the earlier values being relatively large. We’d likely then end up with a value of 0.5 or more.

The key number here is the Pr. The three variants of the K index differ in how it is calculated. Each of them starts by creating a raw frequency distribution of EEIC for a given source to determine an expected probability at a given “score group” r defined by the number of incorrect responses. 

key number

Here, MW refers to the mean number of EEIC for the score group and Ws is still the number of incorrect responses for the source.

The K index (Holland, 1996) uses this raw value. The K1 index applies linear regression to smooth the distribution, and the K2 index applies a quadratic regression to smooth it (Sotaridona & Meijer, 2002); because the regression-predicted value is then used, the notation becomes M-hat.  Since these three then only differ by the amount of smoothing used in an intermediate calculation, the results will be extremely close to one another. This frequency distribution could be calculated based on only examinees in the same location, however, SIFT uses all examinees in the data set, as this would create a more conceptually appealing null distribution.

 

S1 and S2 apply the same framework of the raw frequency distribution of EEIC, but apply it to a different probability calculation instead of using a Poisson model:

S1 index.

S2 is often glossed over in publications as being similar, but it is much more complex.  It contains the Poisson model but calculates the probability of the observed EEIC plus a weighted expectation of observed correct responses in common. This makes much more logical sense because many of the responses that a copier would copy from a smarter student will, in fact, be correct. 

All the other K variants ignore this since it is so much harder to disentangle this from an examinee knowing the correct answer. Sotaridona and Meijer (2003), as well as Sotaridona’s original dissertation, provide treatment on how this number is estimated and then integrated into the Poisson calculations.

The following two tabs change content below.
Avatar for Nathan Thompson, PhD
My Twitter profileMy LinkedIn profileMy YouTube channel

Nathan Thompson, PhD

Nathan Thompson earned his PhD in Psychometrics from the University of Minnesota, with a focus on computerized adaptive testing. His undergraduate degree was from Luther College with a triple major of Mathematics, Psychology, and Latin. He is primarily interested in the use of AI and software automation to augment and replace the work done by psychometricians, which has provided extensive experience in software design and programming. Dr. Thompson has published over 100 journal articles and conference presentations, but his favorite remains https://scholarworks.umass.edu/pare/vol16/iss1/1/ .
/by