One of my graduate school mentors once said in class that there are three standard errors that everyone in the assessment or I/O Psychology field needs to know: the standard error of the mean, the standard error of measurement, and the standard error of the estimate. These concepts are distinct in their purpose and application but can be easily confused by those with minimal training.
Here, I have personally seen the standard error of the mean incorrectly reported as the standard error of measurement, which is a critical mistake in statistical reporting.
In this post, I will briefly describe each of these standard errors to clarify their differences. In future posts, I will explore each in greater depth.
Standard Error of the Mean (SEM)
Is a fundamental concept introduced in introductory statistics courses. It is closely tied to the Central Limit Theorem, which serves as the foundation of statistical analysis. The purpose of this metric is to provide an index of accuracy—or conversely, error—in a sample mean.
Since different samples from a population yield slightly different means, the standard error of the mean estimates the expected variation in sample means. It is calculated using the following formula:
Where:
- SD = Sample standard deviation
- n = Number of observations in the sample
This formula is useful for creating confidence intervals to estimate the true population mean.
Example:
Suppose we conduct a large-scale educational assessment where 50,000 students take a test. The sample mean score is 71, with a standard deviation of 12.3. Applying the formula:
Thus, we can be 95% certain that the true population mean falls within 71 ± 0.055.
Key Takeaway: The standard error of the mean applies to group averages and has nothing to do with psychometricsdirectly. However, it can be used in assessment data when analyzing sample-based studies.
Click here to read more about the standard error of the mean.
Standard Error of Measurement (SEM)
Is particularly important in educational assessment and psychometrics. It estimates the accuracy of an individual’s test score, rather than a group mean.
This error can be calculated using Classical Test Theory (CTT) or Item Response Theory (IRT), though each defines it differently.
Classical Test Theory Formula:
Where:
- SD = Standard deviation of test scores
- r = Reliability of the test
This formula provides an estimate of how much a test-taker’s score would vary if they retook the test multiple times under ideal conditions.
Item Response Theory Perspective:
Under IRT, SEM is not a fixed value but varies across the ability spectrum. A test is more accurate (lower error) in areas where it has more high-quality items. For instance, a test with mostly mid-range difficulty questions will provide more accurate scores in the middle range but be less precise for very high or low scorers.
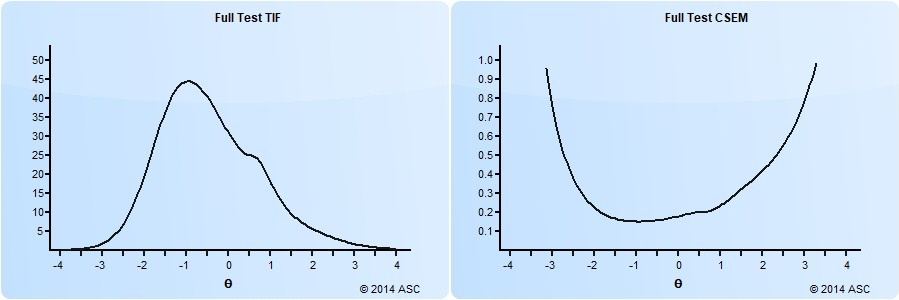
For a deeper discussion of SEM, click here.
Standard Error of the Estimate (SEE)
Measures the accuracy of predictions in linear regression models. It estimates the expected deviation between actual and predicted values.
The formula for SEE is:
Where:
- SD_y = Standard deviation of the dependent variable
- r = Correlation coefficient between predictor and outcome variables
Example:
Imagine we want to predict job performance using a 40-item job knowledge test. We analyze 1,000 job incumbents’ scores and find that those who scored 30/40 had performance ratings ranging from 61 to 89.
Using statistical software (such as Microsoft Excel), we compute:
- SEE = 4.69
- Regression slope = 1.76
- Intercept = 29.93
Using these, the estimated job performance for a test score of 30 is:
To construct a 95% confidence interval:
Resulting in a prediction range of 73.52 to 91.90.
Practical Application:
If an employer wants to hire only candidates likely to score 80 or higher in job performance, they can set a cutscore of 30 on the test based on this estimate.
Key Takeaways: Avoiding Common Mistakes
- The standard error of the mean applies to sample averages and is part of general statistics.
- The standard error of measurement relates to individual test scores and is crucial in assessment and psychometrics.
- The standard error of the estimate is used in predictive modeling (e.g., regression) to assess the accuracy of predictions.
Final Tip: When reporting standard errors in assessment or statistical studies, be sure to use the correct one to maintain accuracy and credibility.
If you found this post helpful, share it with your colleagues or leave a comment below!

Nathan Thompson earned his PhD in Psychometrics from the University of Minnesota, with a focus on computerized adaptive testing. His undergraduate degree was from Luther College with a triple major of Mathematics, Psychology, and Latin. He is primarily interested in the use of AI and software automation to augment and replace the work done by psychometricians, which has provided extensive experience in software design and programming. Dr. Thompson has published over 100 journal articles and conference presentations, but his favorite remains https://scholarworks.umass.edu/pare/vol16/iss1/1/ .

