Coefficient Alpha Reliability Index
Coefficient alpha reliability, sometimes called Cronbach’s alpha, is a statistical index that is used to evaluate the internal consistency or reliability of an assessment. That is, it quantifies how consistent we can expect scores to be, by analyzing the item statistics. A high value indicates that the test is of high reliability, and a low value indicates low reliability. This is one of the most fundamental concepts in psychometrics, and alpha is arguably the most common index. You may also be interested in reading about its competitor, the Split Half Reliability Index.
What is coefficient alpha, aka Cronbach’s alpha?
The classic reference to alpha is Cronbach (1954). He defines it as:
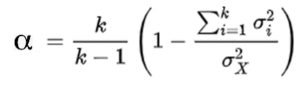
where k is the number of items, sigma-i is variance of item i, and sigma-X is total score variance.
Kuder-Richardson 20
While Cronbach tends to get the credit, to the point that the index is often called “Cronbach’s Alpha” he really did not invent it. Kuder and Richardson (1927) suggested the following equation to estimate the reliability of a test with dichotomous (right/wrong) items.
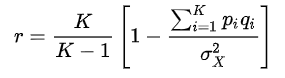
Note that it is the same as Cronbach’s equation, except that he replaced the binomial variance pq with the more general notation of variance (sigma). This just means that you can use Cronbach’s equation on polytomous data such as Likert rating scales. In the case of dichotomous data such as multiple choice items, Cronbach’s alpha and KR-20 are the exact same.
Additionally, Cyril Hoyt defined reliability in an equivalent approach using ANOVA in 1941, a decade before Cronbach’s paper.
How to interpret coefficient alpha
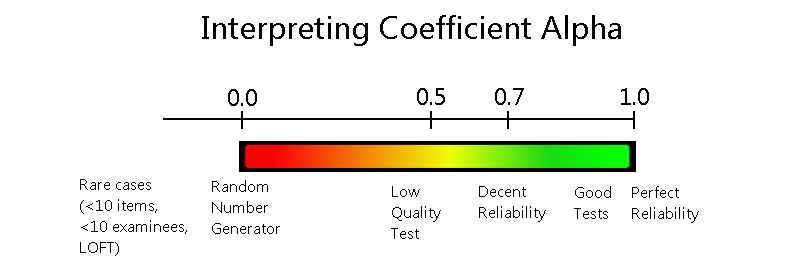
In general, alpha will range from 0.0 (random number generator) to 1.0 (perfect measurement). However, in rare cases, it can go below 0.0, such as if the test is very short or if there is a lot of missing data (sparse matrix). This, in fact, is one of the reasons NOT to use alpha in some cases. If you are dealing with linear-on-the-fly tests (LOFT), computerized adaptive tests (CAT), or a set of overlapping linear forms for equating (non-equivalent anchor test, or NEAT design), then you will likely have a large proportion of sparseness in the data matrix and alpha will be very low or negative. In such cases, item response theory provides a much more effective way of evaluating the test.
What is “perfect measurement?” Well, imagine using a ruler to measure a piece of paper. If it is American-sized, that piece of paper is always going to be 8.5 inches wide, no matter how many times you measure it with the ruler. A bathroom scale is slightly less reliability; You might step on it, see 190.2 pounds, then step off and on again, and see 190.4 pounds. This is a good example of how we often accept unreliability in measurement.
Of course, we never have this level of accuracy in the world of psychoeducational measurement. Even a well-made test is something where a student might get 92% today and 89% tomorrow (assuming we could wipe their brain of memory of the exact questions).
Reliability can also be interpreted as the ratio of true score variance to total score variance. That is, all test score distributions have a total variance, which consist of variance due to the construct of interest (i.e., smart students do well and poor students do poorly), but also some error variance (random error, kids not paying attention to a question, second dimension in the test… could be many things.
What is a good value of coefficient alpha?
As psychometricians love to say, “it depends.” The rule of thumb that you generally hear is that a value of 0.70 is good and below 0.70 is bad, but that is terrible advice. A higher value indeed indicates higher reliability, but you don’t always need high reliability. A test to certify surgeons, of course, deserves all the items it needs to make it quite reliable. Anything below 0.90 would be horrible. However, the survey you take from a car dealership will likely have the statistical results analyzed, and a reliability of 0.60 isn’t going to be the end of the world; it will still provide much better information than not doing a survey at all!
Here’s a general depiction of how to evaluate levels of coefficient alpha.

Using alpha: the classical standard error of measurement
Coefficient alpha is also often used to calculate the classical standard error of measurement (SEM), which provides a related method of interpreting the quality of a test and the precision of its scores. The SEM can be interpreted as the standard deviation of scores that you would expect if a person took the test many times, with their brain wiped clean of the memory each time. If the test is reliable, you’d expect them to get almost the same score each time, meaning that SEM would be small.
SEM=SD*sqrt(1-r)
Note that SEM is a direct function of alpha, so that if alpha is 0.99, SEM will be small, and if alpha is 0.1, then SEM will be very large.
Coefficient alpha and unidimensionality
It can also be interpreted as a measure of unidimensionality. If all items are measuring the same construct, then scores on them will align, and the value of alpha will be high. If there are multiple constructs, alpha will be reduced, even if the items are still high quality. For example, if you were to analyze data from a Big Five personality assessment with all five domains at once, alpha would be quite low. Yet if you took the same data and calculated alpha separately on each domain, it would likely be quite high.
How to calculate the index
Because the calculation of coefficient alpha reliability is so simple, it can be done quite easily if you need to calculate it from scratch, such as using formulas in Microsoft Excel. However, any decent assessment platform or psychometric software will produce it for you as a matter of course. It is one of the most important statistics in psychometrics.
Cautions on overuse
Because alpha is just so convenient – boiling down the complex concept of test quality and accuracy to a single easy-to-read number – it is overused and over-relied upon. There are papers out in the literature that describe the cautions in detail; here is a classic reference.
One important consideration is the over-simplification of precision with coefficient alpha, and the classical standard error of measurement, when juxtaposed to the concept of conditional standard error of measurement from item response theory. This refers to the fact that most traditional tests have a lot of items of middle difficulty, which maximizes alpha. This measures students of middle ability quite well. However, if there are no difficult items on a test, it will do nothing to differentiate amongst the top students. Therefore, that test would have a high overall alpha, but have virtually no precision for the top students. In an extreme example, they’d all score 100%.
Also, alpha will completely fall apart when you calculate it on sparse matrices, because the total score variance is artifactually reduced.
Limitations of coefficient alpha
Cronbach’s alpha has several limitations. Firstly, it assumes that all items on a scale measure the same underlying construct and have equal variances, which is often not the case. Secondly, it is sensitive to the number of items on the scale; longer scales tend to produce higher alpha values, even if the additional items do not necessarily improve measurement quality. Thirdly, Cronbach’s alpha assumes that item errors are uncorrelated, an assumption that is frequently violated in practice. Lastly, it provides only a lower bound estimate of reliability, which means it can underestimate the true reliability of the test.
Summary
In conclusion, coefficient alpha is one of the most important statistics in psychometrics, and for good reason. It is quite useful in many cases, and easy enough to interpret that you can discuss it with test content developers and other non-psychometricians. However, there are cases where you should be cautious about its use, and some cases where it completely falls apart. In those situations, item response theory is highly recommended.
Nathan Thompson, PhD
Latest posts by Nathan Thompson, PhD (see all)
- Psychometrics: Data Science for Assessment - June 5, 2024
- Setting a Cutscore to Item Response Theory - June 2, 2024
- What are technology enhanced items? - May 31, 2024

