The Ebel method of standard setting is a psychometric approach to establish a cutscore for tests consisting of multiple-choice questions. It is usually used for high-stakes examinations in the fields of higher education, medical and health professions, and for selecting applicants.
How is the Ebel method performed?
The Ebel method requires a panel of judges who would first categorize each item in a data set by two criteria: level of difficulty and relevance or importance. Then the panel would agree upon an expected percentage of items that should be answered correctly for each group of items according to their categorization.
It is crucial that judges are the experts in the examined field; otherwise, their judgement would not be valid and reliable. Prior to the item rating process, the panelists should be given sufficient amount of information about the purpose and procedures of the Ebel method. In particular, it is important that the judges would understand the meaning of difficulty and relevance in the context of the current assessment.
Next stage would be to determine what “minimally competent” performance means in the specific case depending on the content. When everything is clear and all definitions are agreed upon, the experts should classify each item across difficulty (easy, medium, or hard) and relevance (minimal, acceptable, important, or essential). In order to minimize the influence of the judges’ opinion on each other, it is more recommended to use individual ratings rather than consensus ones.
Afterwards judgements on the proportion of items expected to be answered correctly by minimally competent candidates need to be collected for each item category, e.g. easy and desirable. However, for the rating and timesaving purposes the grid proposed by Ebel and Frisbie (1972) might be used. It is worth mentioning though that Ebel ratings are content-specific, so values in the grid might happen to be too low or too high for a test.
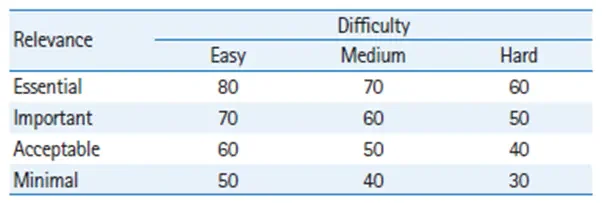
At the end, the Ebel method, like the modified-Angoff method, identifies a cut-off score for an examination based on the performance of candidates in relation to a defined standard (absolute), rather than how they perform in relation to their peers (relative). Ebel scores for each item and for the whole exam are calculated as the average of the scores provided by each expert: the number of items in each category is multiplied by the expected percentage of correct answers, and the total results are added to calculate the cutscore.
Pros of using Ebel
- This method provides an overview of a test difficulty
- Cut-off score is identified prior to an examination
- It is relatively easy for experts to perform
Cons of using Ebel
- This method is time-consuming and costly
- Evaluation grid is hard to get right
- Digital software is required
- Back-up is necessary
Conclusion
The Ebel method is a quite complex standard-setting process compared to others due to the need of an analysis of the content, and it therefore imposes a burden on the standard-setting panel. However, Ebel considers the relevance of the test items and the expected proportion of the correct answers of the minimally competent candidates, including borderline candidates. Thus, even though the procedure is complicated, the results are very stable and very close to the actual cut-off scores.
References
Ebel, R. L., & Frisbie, D. A. (1972). Essentials of educational measurement.

Nathan Thompson earned his PhD in Psychometrics from the University of Minnesota, with a focus on computerized adaptive testing. His undergraduate degree was from Luther College with a triple major of Mathematics, Psychology, and Latin. He is primarily interested in the use of AI and software automation to augment and replace the work done by psychometricians, which has provided extensive experience in software design and programming. Dr. Thompson has published over 100 journal articles and conference presentations, but his favorite remains https://scholarworks.umass.edu/pare/vol16/iss1/1/ .

