The Frary, Tideman, and Watts (1977) g2 index is a collusion (cheating) detection index, which is a standardization that evaluates a number of common responses between two examinees in the typical standardized format: observed common responses minus the expectation of common responses, divided by the expected standard deviation of common responses. It compares all pairs of examinees twice: evaluating examinee copying off b and vice versa.
Frary, Tideman, and Watts (1977) g2 Index
The g2 collusion index starts by finding the probability, for each item, that the Copier would choose (based on their ability) the answer that the Source actually chose. The sum of these probabilities than the expected number of equivalent responses. We can then compare this to the actual observed number of equivalent responses and standardize that difference with the standard deviation. A very positive value could be possibly indicative of copying.
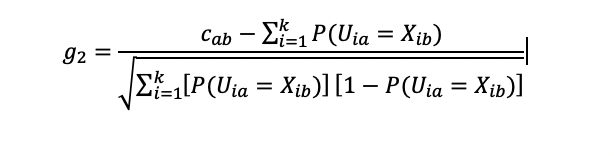
Where
Cab = Observed number of common responses (e.g., both examinees selected answer D)
k = number of items i
Uia = Random variable for examinee a’s response to item i
Xia = Observed response of examinee b to item i.
Frary et al. estimated P using classical test theory, and the definitions are provided in the original paper, while a slightly more clear definitions are provided in Khalid, Mehmood, and Rehman (2011).
The g2 approach produces two half-matrices, which SIFT presents as a single matrix separated by a blank diagonal. That is, the lower half of the matrix evaluates whether examinee a copied off b, and the upper half whether b copied off a. More specifically, the row number is the copier and the column number is the source. So Row1/Column2 evaluates whether 1 copied off 2, while Row2/Column1 evaluates whether 2 copied off 1.
For g2 and Wollack’s (1997) ω, the flagging procedure counts all values in the matrix greater than the critical value, so it is possible – likely actually – that each pair will be flagged twice. So the numbers in those flag total columns will be greater than those in the unidirectional indices.
How to interpret? This collusion index is standardized onto a z-metric, and therefore can easily be converted to the probability you wish to use. A standardized value of 3.09 is default for g2, ω, and Zjk because this translates to a probability of 0.001. A value beyond 3.09 then represents an event that is expected to be very rare under the assumption of no collusion.
Want to implement this statistic? Download the SIFT software for free.

Nathan Thompson earned his PhD in Psychometrics from the University of Minnesota, with a focus on computerized adaptive testing. His undergraduate degree was from Luther College with a triple major of Mathematics, Psychology, and Latin. He is primarily interested in the use of AI and software automation to augment and replace the work done by psychometricians, which has provided extensive experience in software design and programming. Dr. Thompson has published over 100 journal articles and conference presentations, but his favorite remains https://scholarworks.umass.edu/pare/vol16/iss1/1/ .
