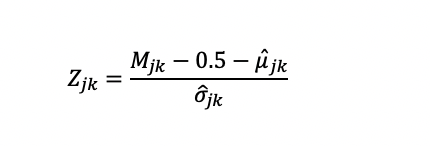
Wesolowsky (2000) Zjk Collusion Detection Index

Wesolowsky’s (2000) index is a collusion detection index, designed to look for exam cheating by finding similar response vectors amongst examinees. It is in the same family as g₂ and Wollack’s ω.  Like those, it creates a standardized statistic by evaluating the difference between observed and expected common responses and dividing by a standard error.  It is more similar to the g₂ index in that it is based on classical test theory rather than item response theory.  This has the advantage of being conceptually simpler as well as more feasible for small samples (it is well-known that IRT requires minimum sample sizes of 100 to 1000 depending on the model).  However, this of course means that it lacks the conceptual, theoretical, and mathematical appropriateness of IRT, which is the dominant psychometric paradigm for large-scale tests for good reason.

Wesolowsky defined his collusion detection index as

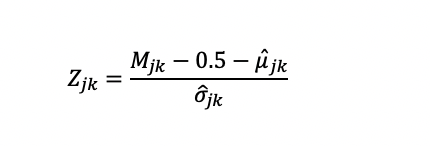
where

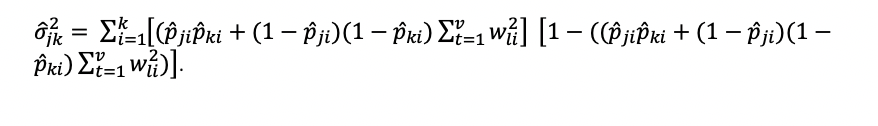
Here, the expected number of common responses  is equal to the joint probability of each examinee (j and k) getting item i correct, plus both getting it incorrect with the same distractor t selected.  This is calculated as a single probability for each item then summed across items.  The probability for each item is then of course multiplied by one minus itself to create a binomial variance.

The major difference between this and g₂ is that g₂ estimated the probability using a piecewise linear function that grossly approximated an item response function from IRT.  Wesolowsky utilized a curvilinear function he called “iso-contours” which is better in that it is curvilinear, but it is still not on par with the item response function in terms of conceptual appropriateness.  The iso-contours are described by a parameter Wesolowsky referred to as a (completely unrelated to the IRT discrimination parameter), which must be estimated by bisection approximation.

How to interpret?  This index is standardized onto a z-metric, and therefore can easily be converted to the probability you wish to use.  A standardized value of 3.09 is default for g₂, ω, and Z_jk because this translates to a probability of 0.001.  A value beyond 3.09 then represents an event that is expected to be very rare under the assumption of no collusion.

Want to calculate this index? Download the free program SIFT.

The following two tabs change content below.

• Bio
• Latest Posts

Nathan Thompson, PhD

Nathan Thompson earned his PhD in Psychometrics from the University of Minnesota, with a focus on computerized adaptive testing. His undergraduate degree was from Luther College with a triple major of Mathematics, Psychology, and Latin. He is primarily interested in the use of AI and software automation to augment and replace the work done by psychometricians, which has provided extensive experience in software design and programming. Dr. Thompson has published over 100 journal articles and conference presentations, but his favorite remains https://scholarworks.umass.edu/pare/vol16/iss1/1/ .

Latest posts by Nathan Thompson, PhD (see all)

• What is an Assessment-Based Certificate? - October 12, 2024
• What is Psychometrics? How does it improve assessment? - October 12, 2024
• What is RIASEC Assessment? - September 29, 2024