Wollack 1997 Omega Collusion Index

Wollack (1997) adapted the standardized collusion index of Frary, Tidemann, and Watts (1977) g₂ to item response theory (IRT) and produced the Wollack Omega (ω) index.  It is clear that the graphics in the original article by Frary, Tideman, and Watts (1977) were crude classical approximations of an item response function, so Wollack replaced the probability calculations from the classical approximations with those from IRT. 

The probabilities could be calculated with any IRT model.  Wollack suggested Bock’s Nominal Response Model since it is appropriate for multiple-choice data, but that model is rarely used in practice and very few IRT software packages support it.  SIFT instead supports the use of dichotomous models: 1-parameter, 2-parameter, 3-parameter, and Rasch.

Because of using IRT, implementation of ω requires additional input.  You must include the IRT item parameters in the control tab, as well as examinee theta values in the examinee tab.  If any of that input is missing, the omega output will not be produced.

The ω index is defined as

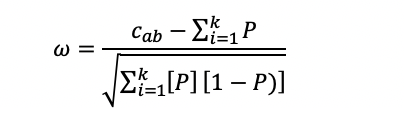
Where P is the probability of an examinee with θ_a selecting the response, that examinee b selected, and c_ab is the Responses in Common (RIC) Index.  That is, the probability that the copier with θa would select the responses that the source did when summed, this can be interpreted as the expected RIC. 

Note: This uses all responses, not just errors.

How to interpret?  The value will be higher when the copier had more responses in common with the source than we’d expect from a person of that (probably lower) ability.  This index is standardized onto a z-metric, and therefore can easily be converted to the probability you wish to use. 

A standardized value of 3.09 is the default for g₂, ω, and Z_jk Collusion Detection Index because this translates to a probability of 0.001.  A value beyond 3.09, then, represents an event that is expected to be very rare under the assumption of no collusion.

Interested in applying the Wollack Omega index to your data? Download the SIFT software for free.

The following two tabs change content below.

• Bio
• Latest Posts

Nathan Thompson, PhD

Nathan Thompson earned his PhD in Psychometrics from the University of Minnesota, with a focus on computerized adaptive testing. His undergraduate degree was from Luther College with a triple major of Mathematics, Psychology, and Latin. He is primarily interested in the use of AI and software automation to augment and replace the work done by psychometricians, which has provided extensive experience in software design and programming. Dr. Thompson has published over 100 journal articles and conference presentations, but his favorite remains https://scholarworks.umass.edu/pare/vol16/iss1/1/ .

Latest posts by Nathan Thompson, PhD (see all)

• What is an Assessment-Based Certificate? - October 12, 2024
• What is Psychometrics? How does it improve assessment? - October 12, 2024
• What is RIASEC Assessment? - September 29, 2024