The IRT Item Pseudo-guessing Parameter
Content
The item pseudo-guessing parameter is one of the three item parameters estimated under item response theory (IRT): discrimination a, difficulty b, and pseudo-guessing c. The parameter that is utilized only in the 3PL model is the pseudo-guessing parameter c. It represents a lower asymptote for the probability of an examinee responding correctly to an item.
Background of IRT item pseudo-guessing parameter
If you look at the post on the IRT 2PL model, you will realize that the probability of a response depends on the examinee ability level θ, the item discrimination parameter a, and the item difficulty parameter b. However, one of the realities in testing is that examinees will get some multiple-choice items by guessing. Therefore, the probability of the correct response might include a small component that is guessing.
Neither 1PL, nor 2PL considered guessing phenomenon, but Birnbaum (1968) altered the 2PL model to include it. Unfortunately, due to this inclusion the logistic function from the 2PL model lost its nice mathematical properties. Nevertheless, even though it is no longer a logistic model in a technical aspect, it has become known as the three-parameter logistic model (3PL or IRT 3PL). Baker (2001) suggested the following equation for the IRT 3PL model
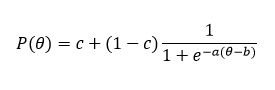
where:
a is the item discrimination parameter
b is the item difficulty parameter
c is the item pseudo-guessing parameter
θ is the examinee ability parameter
Interpretation of pseudo-guessing parameter
In general, the pseudo-guessing parameter c is the probability of getting the item correct by guessing alone. For instance, c = 0.20 means that at all ability levels, the probability of getting the item correct by guessing alone is 0.20. This very often reflects the structure of multiple choice items: 5-options items will tend to have values around 0.20 and 4-option items around 0.25.
It is worth noting, that the value of c does not vary as a function of the trait/ability level θ, i.e. examinees with high and low ability levels have the same probability of responding correctly by guessing. Theoretically, the guessing parameter ranges between 0 and 1, but practically values above 0.35 are considered inacceptable, hence the range 0 < c < 0.35 is applied. A value higher than 1/k, where k is the number of options, often indicates that a distractor is not performing.
How pseudo-guessing parameter affects other parameters
Due to the presence of the guessing parameter, the definition of the item difficulty parameter b is changed. Within the 1PL and 2PL models, b is the point on the ability scale at which the probability of the correct response is 0.5. Under the 3PL model, the lower limit of the item characteristic curve (ICC) or item response function (IRF) is the value of c rather than zero. According to Baker (2001), the item difficulty parameter is the point on the ability scale where:
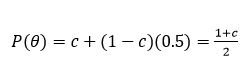
Therefore, the probability is halfway between the value of c and 1. Thus, the parameter c has defined a boundary to the lowest value of the probability of the correct response, and the item difficulty parameter b determines the point on the ability scale where the probability of the correct response is halfway between this boundary and 1.
The item discrimination parameter a can still be interpreted as being proportional to the slope of the ICC/IRF at the point θ = b. However, under the 3PL model, the slope of the ICC/IRF at θ = b actually equals to a×(1−c)/4. These changes in the definitions of the item parameters a and b are quite important when interpreting test analyses.
References
Baker, F. B. (2001). The basics of item response theory.
Birnbaum, A. L. (1968). Some latent trait models and their use in inferring an examinee’s ability. In F. M. Lord & M. R. Novick (Eds.), Statistical theories of mental test scores (pp. 395–479). Addison-Wesley.
Laila Issayeva M.Sc.
Latest posts by Laila Issayeva M.Sc. (see all)
- What is a z-score? - November 28, 2024
- Confidence Intervals in Assessment and Psychometrics - November 25, 2024
- General Intelligence and Its Role in Assessment and Measurement - November 10, 2024
