The One Parameter Logistic Model
The One Parameter Logistic Model (OPLM or 1PL or IRT 1PL) is one of the three main dichotomous models in the Item Response Theory (IRT) framework. The OPLM combines mathematical properties of the Rasch model with the flexibility of the Two Parameter Logistic Model (2PL or IRT 2PL). In the OPLM, difficulty parameters, b, are estimated and discrimination indices, a, are imputed as known constants.
Background behind the One Parameter Logistic Model
IRT employs mathematical models assuming that the probability that an examinee would answer the question correctly depends on their ability and item characteristics. Examinee’s ability is considered the major individual characteristic and is denoted as θ (“theta”); it is also called the ability parameter. The ability parameter is conceived as an underlying, unobservable latent construct or trait that helps an individual to answer a question correctly.
These mathematical models include item characteristics also known as the item parameters: discrimination (a), difficulty (b), and pseudo-guessing (c). According to IRT paradigm, all item parameters are considered to be invariant or “person-free”, i.e. they do not depend on examinees’ abilities. In addition, ability estimates are also invariant or “item-free” since they do not depend on the set of items. This mutual independence forms the basis of the IRT models that provides objectivity in measurement.
The OPLM is built off only one parameter, difficulty. Item difficulty simply means how hard an item is (how high does the latent trait ability level need to be in order to have a 50% chance of getting the item right?). b is estimated for each item of the test. The item response function for the 1PL model looks like this:
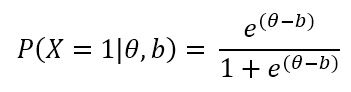
where P is the probability that a randomly selected examinee with ability θ will answer correctly a specific item; e is a mathematical constant approximately equal to 2.71828, which is also known as an exponential number or Euler’s number.
Assumptions of the OPLM
The OPLM is based on two basic assumptions: unidimensionality and local independence.
- Unidimensionality assumption is the most common, but the most complex and restrictive assumption for all IRT models that sometimes cannot be met. It states that only one ability is measured by the set of items in a single test. Thus, it assumes that a single dominant factor should underlie all item responses. For example, in a Math test examinees need to possess strong mathematical abilities to answer test questions correctly. However, if test items measure another ability, like verbal, this test is no longer unidimensional. The unidimensionality can be assessed by various methods, but the most popular among all is the factor analysis approach which is available in the free software MicroFACT.
- Local independence assumes that in case of a constant ability, examinee’s responses to any items are statistically independent, i.e. the probability that an examinee would reply correctly to a test question does not depend on their answers to other questions. In other words, the only factor influencing examinee’s responses is the ability.
Item characteristic curve
The S-shaped curve describing the relationship between the probability of an examinee’s correct response to a test question and their ability θ is called item characteristic curve (ICC) or item response function (IRF). In a test, each item will have its own ICC/IRF.
Typical ICC for the One Parameter Logistic Model looks like this:
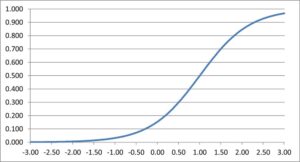
The S-shaped curve shows that the probability of a correct response is near zero at the lowest level of examinee’s ability and increases up to the highest level of ability as the probability of correct response approaches 1. The curve rises rapidly as we move from left to right and is strictly monotonic.
The OPLM function ranges between 0 and 1. ICC can never reach and cannot be higher than 1. Theoretically, item parameter ranges from -∞ to + ∞ but practically this range is limited between -3 and +3. You can easily plot ICC using the IRT calibration software Xcalibre.
Application of the OPLM in test development
The OPLM is especially useful in item selection, item banking, item analysis, test equating, and investigating item bias or Differential Item Functioning (DIF). Since the IRT One Parameter Logistic Model allows estimating item parameters that are “examinee-free”, then it is possible to estimate item parameters during their piloting to use them later. Based on the information about items and examinees collected during tests it is easy to build item banks that can be ultimately used for large-scale testing programs and Computerized Adaptive Testing (CAT).
Laila Baudinovna Issayeva M.Sc.
Latest posts by Laila Baudinovna Issayeva M.Sc. (see all)
- Digital Badges - May 29, 2023
- The Graded Response Model – Samejima (1969) - May 10, 2023
- What ChatGPT brings us for item writing - April 9, 2023
