Test response function 10 items Angoff

Setting a Cutscore to Item Response Theory

Nathan Thompson, PhDJune 2, 2024

Setting a cutscore on a test scored with item response theory (IRT) requires some psychometric knowledge.  This post will get you started.

How do I set a cutscore with item response theory?

There are two approaches: directly with IRT, or using CTT then converting to IRT.

  1. Some standard setting methods work directly with IRT, such as the Bookmark method.  Here, you calibrate your test with IRT, rank the items by difficulty, and have an expert panel place “bookmarks” in the ranked list.  The average IRT difficulty of their bookmarks is then a defensible IRT cutscore.  The Contrasting Groups method and the Hofstee method can also work directly with IRT.
  2. Cutscores set with classical test theory, such as the Angoff, Nedelsky, or Ebel methods, are easy to implement when the test is scored classically.  But if your test is scored with the IRT paradigm, you need to convert your cutscores onto the theta scale.  The easiest way to do that is to reverse-calculate the test response function (TRF) from IRT.

The Test Response Function

The TRF (sometimes called a test characteristic curve) is an important method of characterizing test performance in the IRT paradigm.  The TRF predicts a classical score from an IRT score, as you see below.  Like the item response function and test information function (item response and test information function), it uses the theta scale as the X-axis.  The Y-axis can be either the number-correct metric or proportion-correct metric.

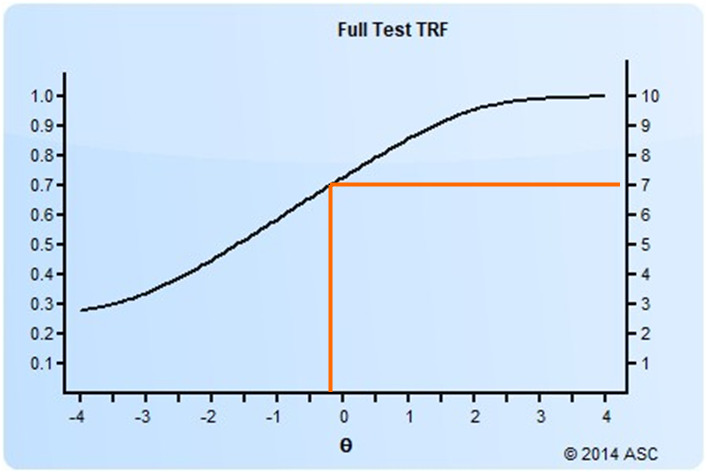
Test response function 10 items Angoff

In this example, you can see that a theta of -0.3 translates to an estimated number-correct score of approximately 7, or 70%.

Classical cutscore to IRT

So how does this help us with the conversion of a classical cutscore?  Well, we hereby have a way of translating any number-correct score or proportion-correct score.  So any classical cutscore can be reverse-calculated to a theta value.  If your Angoff study (or Beuk) recommends a cutscore of 7 out of 10 points (70%), you can convert that to a theta cutscore of -0.3 as above.  If the recommended cutscore was 8 (80%), the theta cutscore would be approximately 0.7.

Because IRT works in a way that it scores examinees on the same scale with any set of items, as long as those items have been part of a linking/equating study.  Therefore, a single study on a set of items can be equated to any other linear test form, LOFT pool, or CAT pool.  This makes it possible to apply the classically-focused Angoff method to IRT-focused programs.  You can even set the cutscore with a subset of your item pool, in a linear sense, with the full intention to apply it on CAT tests later.

Note that the number-correct metric only makes sense for linear or LOFT exams, where every examinee receives the same number of items.  In the case of CAT exams, only the proportion correct metric makes sense.

How do I implement IRT?

Interested in applying IRT to improve your assessments?  Download a free trial copy of  Xcalibre  here.  If you want to deliver online tests that are scored directly with IRT, in real time (including computerized adaptive testing), check out  FastTest.

The following two tabs change content below.
Avatar for Nathan Thompson, PhD
My Twitter profileMy LinkedIn profileMy YouTube channel

Nathan Thompson, PhD

Nathan Thompson earned his PhD in Psychometrics from the University of Minnesota, with a focus on computerized adaptive testing. His undergraduate degree was from Luther College with a triple major of Mathematics, Psychology, and Latin. He is primarily interested in the use of AI and software automation to augment and replace the work done by psychometricians, which has provided extensive experience in software design and programming. Dr. Thompson has published over 100 journal articles and conference presentations, but his favorite remains https://scholarworks.umass.edu/pare/vol16/iss1/1/ .
/by