The Rasch model

The Rasch model, also known as the one-parameter logistic model, was developed by Danish mathematician Georg Rasch and published in 1960.  Over the ensuing years it has attracted many educational measurement specialists and psychometricians because of its simplicity and ease of computational implementation.  Indeed, since it predated the availability of computers for test development work, it was capable of being implemented using simple calculating equipment available at that time.  The original model, developed for achievement and ability tests scored correct or incorrect, or for dichotomously scored personality or attitude scales, has since been extended into a family of models that work with polytomously scored data, rating scales, and a number of other measurement applications. The majority of those models maintain the simplicity of the original model proposed by Rasch.

In 1960, the Rasch model represented a step forward from classical test theory that had then been the major source of methods for test and scale development, and measuring individual differences, since the early 1900s.  The model was accepted by some educational measurement specialists because of its simplicity, its relative ease of implementation, and most importantly because it maintained the use of the familiar number-correct score to quantify an individual’s performance on a test.  Beyond serving as a bridge from classical test methods, the Rasch model is notable as the first formal statement of what, about ten years later, would be known as item characteristic curve theory or item response theory (IRT).  As an IRT model, the Rasch model placed persons and items on the same scale, and introduced concepts such as item information, test information, conditional standard error of measurement, maximum likelihood estimation, and model fit. Furthermore, the evolution of IRT has given rise to multidimensional item response theory (MIRT), which extends these concepts to accommodate multiple latent traits.

What is the Rasch Model?

As an IRT model, the dichotomous Rasch model can be expressed as an equation,

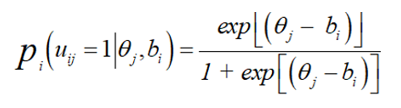
This equation defines the item response function (or item characteristic curve) for a single test item.  It states that the probability (p_i) of a correct (or keyed) response (u_ij = 1) to an item (i), given a trait level (q_j) for a person and the difficulty of an item (b_j), is an exponential function of the difference between a person’s trait level and the difficulty of an item.  If the difference between those two terms is zero, the probability is 0.50.  If the person is “above” the item (the item is easy for the person) the probability is greater than 0.50; if the person is “below” the item (the item is difficult for the person) the probability will be less than .50.  The probability correct, therefore, varies with the distance between the person and the item. This characteristic of the Rasch model is found, with some important modifications, in all later IRT models.

Assumptions of the Rasch Model

Based on the above equation, the Rasch model can be seen to make some strong assumptions.  It obviously assumes that the only characteristic of test items that affects a person’s response to the item is its difficulty.  But anyone who has ever done a classical item analysis has observed that items also vary in their discriminations—frequently markedly so.  Yet the Rasch model ignores that information and assumes that all test items have a constant discrimination.  Also, when used with multiple-choice items (or worse, true-false or other items with only two alternatives) guessing can also affect how examinees answer test items—yet the Rasch model also ignores guessing.

Because the model assumes that all items have the same discriminations, it allows examinees to be scored by number correct. But like classical test scoring methods using number-correct scores, their use results in a substantial loss of capability of reflecting individual differences among examinees by using number-correct scoring.  For example, a 6-item number-correct scored test (too short to be useful) can make seven distinctions among a group of examinees, regardless of group size, whereas a more advanced IRT model can make 64 distinctions among those examinees by taking response pattern into account (i.e., which questions were answered correctly and which incorrectly); a 20-item test scored by number-correct results in 21 possible scores—again regardless of group size—whereas non-Rasch IRT scoring will result in 1,048,576 potentially different scores.

Perspectives on the Model

Although the Rasch model is the simplest case of more advanced IRT models, it incorporates a fundamental difference from its more realistic expansions—the two-, three- and four-parameter logistic (or normal ogive) models for dichotomously scored items.  Applications of the Rasch model assume that the model is correct and that observed data must fit the model, Thus, items whose discriminations are not consistent with the model are eliminated in the construction of a measuring instrument.  Similarly, in estimating latent trait scores for examinees, examinees whose responses do not fit the model are eliminated from the calibration data analysis. By contrast, the more advanced and flexible IRT models fit the model to the data.  Although they evaluate model fit for each item (and similarly can evaluate it for each person) the model fit to a given dataset (whether it has two, three, or four item parameters) is the model that best fits that data.  This philosophical—and operational—difference between the Rasch and the other IRT models has important practical implications for the outcome of the test development process.

The Rasch Model and other IRT Models

Although the Rasch model was an advancement is psychometrics in 1960, over the last 60 years it has been replaced by more general models that allow test items to vary in discrimination, guessing, and a fourth parameter.  With the development of powerful computing capabilities, IRT has given rise to a wide-ranging family of models that function flexibly with ability, achievement, personality, attitude, and other educational and psychological variables.  These IRT models are easily implemented with a variety of readily available software packages, and are based on models that can be fit to unidimensional or multidimensional datasets, model response times, and in many respects vastly improve the development of measuring instruments and measurement of individual differences.  Given these advanced IRT models, the Rasch model can best be viewed as an early historical footnote in the history of modern psychometrics.

Implementing the Rasch Model

You will need specialized software.  The most common is WINSTEPS.  You might also be interested in  Xcalibre  (download trial version for free).

The following two tabs change content below.

• Bio
• Latest Posts

David Weiss

David J. Weiss, PhD, is a professor at the University of Minnesota, where he was Director of the Psychometrics Methods program for several decades. During that time, he led the much of the seminal research behind Computerized Adaptive Testing, and trained several generations of eminent psychometricians.

Latest posts by David Weiss (see all)

• The Rasch model - September 13, 2021