Item response theory (IRT) is an extremely powerful psychometric paradigm that addresses many of the inadequacies of classical test theory (CTT). If you are new to the topic, there is a broad intro here, where you will learn that IRT is actually a family of mathematical models rather than one specific one. Today, I’m talking about the 3PL.
One of the most commonly used models is called the three parameter IRT model (3PM), or the three parameter logistic model (3PL or 3PLM) because it is almost always expressed in a logistic form. The equation for this is below (Hambleton & Swaminathan, 1985, Eq. 3.3).
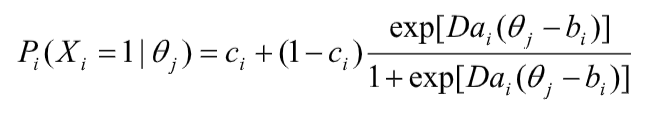
Like all IRT models, it is seeking to predict the probability of a certain response based on examinee ability/trait level and some parameters which describe the performance of the item. With the 3PL, those parameters are a (discrimination), b (difficulty or location), and c (pseudo-guessing). For more on these, check out the descriptions in my general IRT article.
The remaining point then is what we mean by the probability of a certain response. The 3PL is a dichotomous model which means that it is predicting a binary outcome such as correct/incorrect or agree/disagree.
When should I use the three parameter IRT model?
The applicability of the 3PL to a certain assessment depends on the relevance of the components just discussed. First, the response to the items must be binary. This eliminates Likert-type items (“Rate on a scale of 1 to 5”), partial credit items (scoring an essay as 0 to 5 points), and performance assessments where scoring might include a range of points, deductions, or timing (number of words typed per minute).
Next, you should evaluate the applicability of the use of all three parameters. Most notably, are the items in your assessment susceptible to guessing? Because the thing that differentiates the 3PL from its sisters the 1PL and 2PL is that it attempts to model for guessing. This, of course, is highly relevant for multiple-choice items on knowledge or ability assessments, so the 3PL is often a great fit for those.
Even in this case, though, there are a number of practitioners and researchers that still prefer to use the 1PL or 2PL models. There are some deeper methodological issues driving this choice. The 2PL is sometimes chosen because it works well with an estimation method called Joint Maximum Likelihood.
The 1PL, also known as the Rasch model (yes, I know the Rasch people will say they are not the same, I am grouping them together for simplicity in comparison), is often selected because adherents to the model believe in certain advantages such as it providing “objective measurement.” Also, the Rasch model works far better for smaller samples (see this technical report by Guyer & Thompson and this one by Yoes). Regardless, you should probably evaluate model fit when selecting models.
I am from a camp that is pragmatic in choice rather than dogmatic. While training on the 3PL in graduate school, I have no qualms against using the 2PL or 1PL/Rasch if the test type and sample size warrant it or if fit statistics indicate they are sufficient.
How do I implement the three parameter IRT model?
If you want to implement the three parameter IRT model, you need specialized software. General statistical software such as SPSS does not always produce IRT analysis, though some do. Even in the realm of IRT-specific software, not all produce the 3PL. And, of course, the software can vary greatly in terms of quality. Here are three important ways it can vary:
- Accuracy of results: check out this research study which shows that some programs are inaccurate
- User-friendliness: some programs require you to write extensive code, and some have a purely graphical interface
- Output usability and interpretability: some programs just give simple ASCII text, others provide extensive Word or HTML reports with many beautiful tables and graphs.
For more on this topic, head over to my post on how to implement IRT in general.
Want to get started immediately? Download a free copy of our IRT software Xcalibre.

Nathan Thompson earned his PhD in Psychometrics from the University of Minnesota, with a focus on computerized adaptive testing. His undergraduate degree was from Luther College with a triple major of Mathematics, Psychology, and Latin. He is primarily interested in the use of AI and software automation to augment and replace the work done by psychometricians, which has provided extensive experience in software design and programming. Dr. Thompson has published over 100 journal articles and conference presentations, but his favorite remains https://scholarworks.umass.edu/pare/vol16/iss1/1/ .

