Test Development

The Story of the Three Standard Errors
One of my graduate school mentors once said in class that there are three standard errors that everyone in the assessment or I/O Psychology field needs to know: the standard error of the mean, the

Digital Literacy Assessment and its Role in Modern Education
Digital literacy assessments are a critical aspect of modern educational and workforce development initiatives, given today’s fast-paced and technology-driven world, where digital literacy is essential in one’s education, occupation, and even in daily life. Defined

Summative vs Formative Assessment in Education
Summative and formative assessment are a crucial component of the educational process. If you work in the educational assessment field or even in educational generally, you have probably encountered these terms. What do they mean?
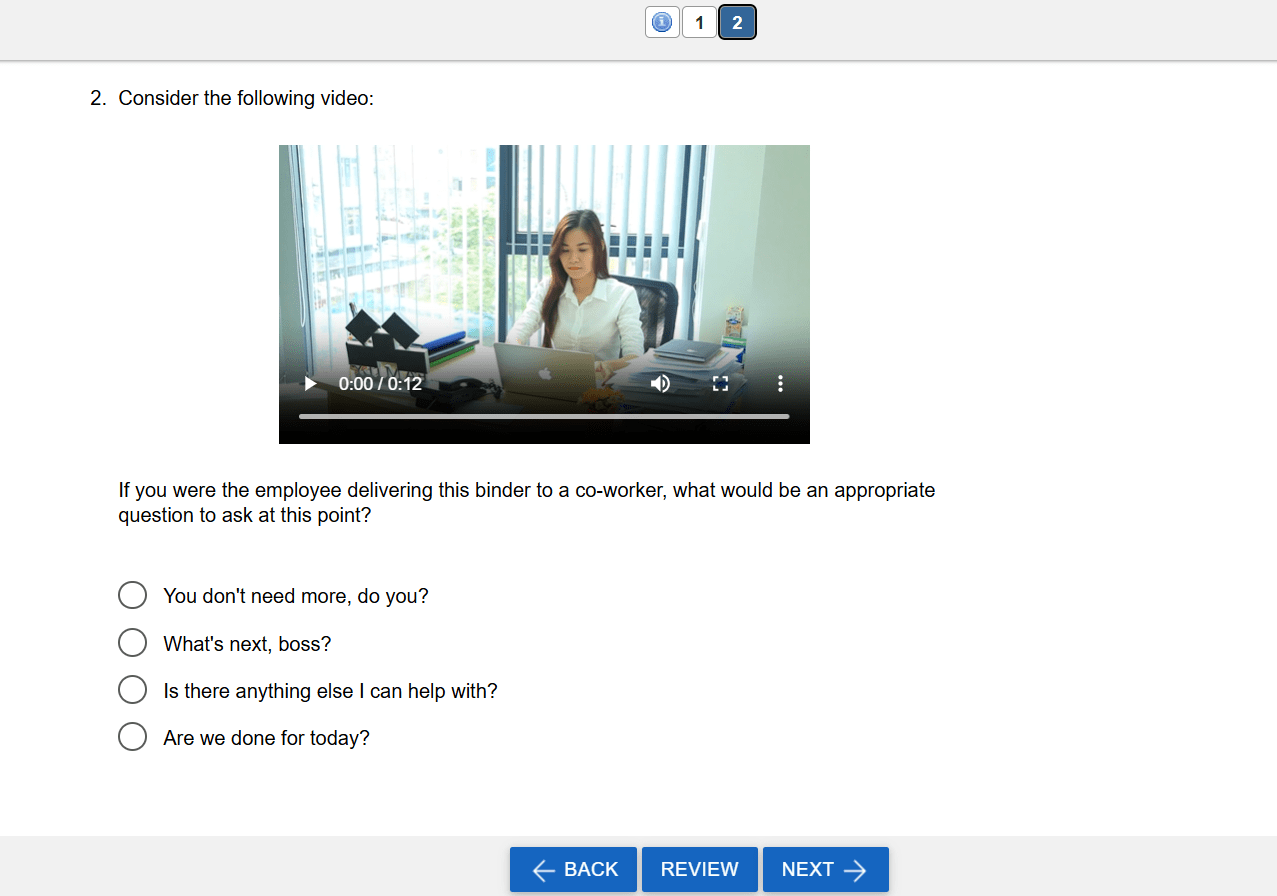
Situational Judgment Tests: Higher Fidelity in Pre-Employment Testing
Situational judgment tests (SJTs) are a type of assessment typically used in a pre-employment context to assess candidates’ soft skills and decision-making abilities. As the name suggests, we are not trying to assess something like
What is a z-score?
A z-score measures the distance between a single person’s raw score and a raw score mean in standard deviation units. It conveys the location of an observation in a normal distribution, of which scores on

Confidence Intervals in Assessment and Psychometrics
Confidence intervals (CIs) are a fundamental concept in statistics, used extensively in assessment and measurement to estimate the reliability and precision of data. Whether in scientific research, business analytics, or health studies, confidence intervals provide

General Intelligence and Its Role in Assessment and Measurement
General intelligence, often symbolized as “g,” is a concept that has been central to psychology and cognitive science since the early 20th century. First introduced by Charles Spearman, general intelligence represents an individual’s overall cognitive

Speeded Test vs Power Test
The concept of Speeded vs Power Test is one of the ways of differentiating psychometric or educational assessments. In the context of educational measurement and depending on the assessment goals and time constraints, tests are

Certification vs. Licensure Exams: Differences and Examples
Certification vs licensure refers to the organization that runs a credentialing exam, usually nonprofit vs government, and whether it is legally required. These are terms that are used quite frequently to refer to credentialing examinations

Factor Analysis: Evaluating Dimensionality in Assessment
Factor analysis is a statistical technique widely used in research to understand and evaluate the underlying structure of assessment data. In fields such as education, psychology, and medicine, this approach to unsupervised machine learning helps
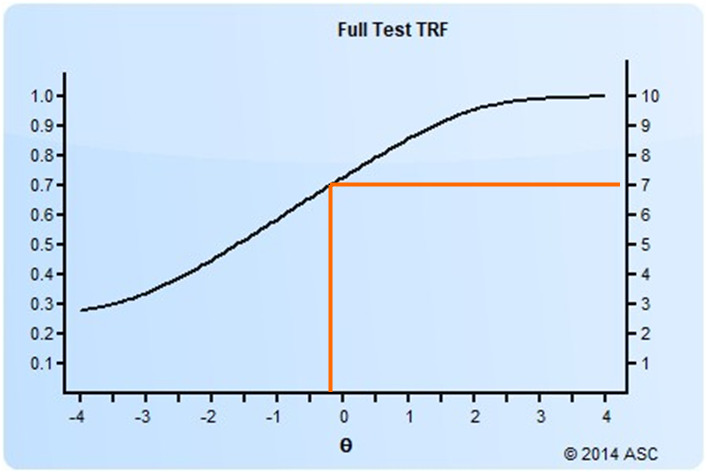
Setting a Cutscore to Item Response Theory
Setting a cutscore on a test scored with item response theory (IRT) requires some psychometric knowledge. This post will get you started. How do I set a cutscore with item response theory? There are two
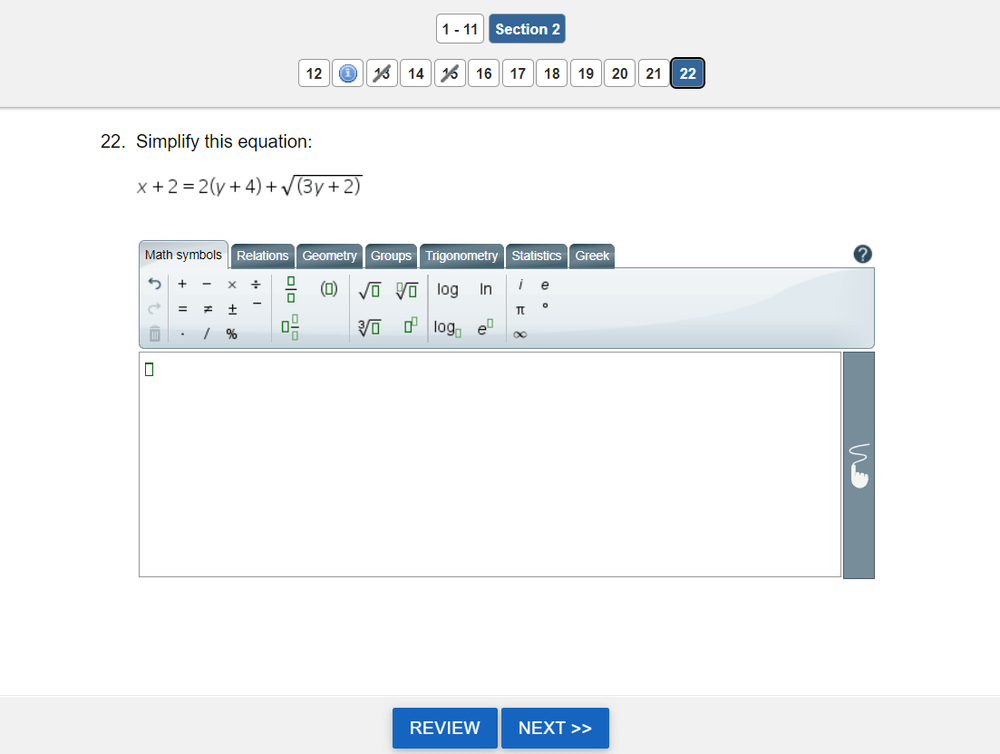
What are technology enhanced items?
Technology-enhanced items are assessment items (questions) that utilize technology to improve the interaction of a test question in digital assessment, over and above what is possible with paper. Tech-enhanced items can improve examinee engagement (important
Modified-Angoff Method Study
A modified-Angoff method study is one of the most common ways to set a defensible cutscore on an exam. It therefore means that the pass/fail decisions made by the test are more trustworthy than if
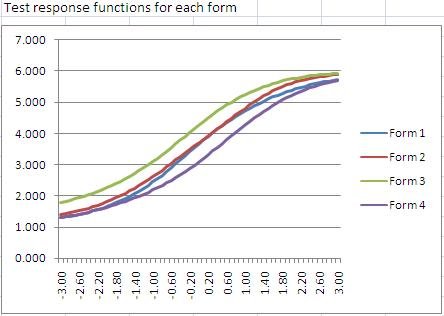
What is Item Response Theory (IRT)?
Item response theory (IRT) is a family of machine learning models in the field of psychometrics, which are used to design, analyze, validate, and score assessments. It is a very powerful psychometric paradigm that revolutionized

Why PARCC EBSR Items Provide Bad Data
The Partnership for Assessment of Readiness for College and Careers (PARCC) is a consortium of US States working together to develop educational assessments aligned with the Common Core State Standards. This is a daunting task,

What is Test Scaling?
Scaling is a psychometric term regarding the establishment of a score metric for a test, and it often has two meanings. First, it involves defining the method to operationally scoring the test, establishing an underlying

How to develop and roll out a Certification Test
Certification test development refers to the process of building an exam in accordance to international standards like NCCA, then delivering it securely. It is a critical business need for credentialing organizations and awarding bodies. As

Innovation in Assessment: Learning from Other Industries
One of my favorite quotes is from Mark Twain: “There is no such thing as a new idea. It is impossible. We simply take a lot of old ideas and put them into a sort
