z-score-avatar

What is a z-score?

Laila Issayeva M.Sc.November 15, 2023

A z-score measures the distance between a raw score and a mean in standard deviation units. The z-score is also known as a standard score since it enables comparing scores on various variables by standardizing the distribution of scores. It is worth mentioning that a standard normal distribution (also known as the z-score distribution or probability distribution) is a normally shaped distribution with a mean of 0 and a standard deviation of  1. T-score is another example of standardized scores.

The z-score can be positive or negative. The sign depends on whether the observation is above or below the mean. For instance, the z of  +2  indicates that the raw score (data point) is two standard deviations above the mean, while a  -1  signifies that it is one standard deviation below the mean. The z of 0 equals the mean. Z-scores generally range from  -3  standard deviations (which would fall to the far left of the normal distribution curve) up to  +3  standard deviations (which would fall to the far right of the normal distribution curve). This covers  99%  of the population; there are people outside that range (e.g., gifted students) but for most cases it is difficult to measure the extremes and there is little practical difference.  It is for this reason that scaled scores on exams are often produced with this paradigm; the SAT has a mean of  500  and standard deviation of  100, so the range is  200  to  800. 

How to calculate a z-score

Here is a formula for calculating the z:

z = (x – μ)/σ

where

     x – individual value

     μ – mean

     σ – standard deviation.

Interpretation of the formula:

  • Subtract the mean of the values from the individual value
  • Divide the difference by the standard deviation.

Here is a graphical depiction of the standard normal curve and how the z-score relates to other metrics.

 

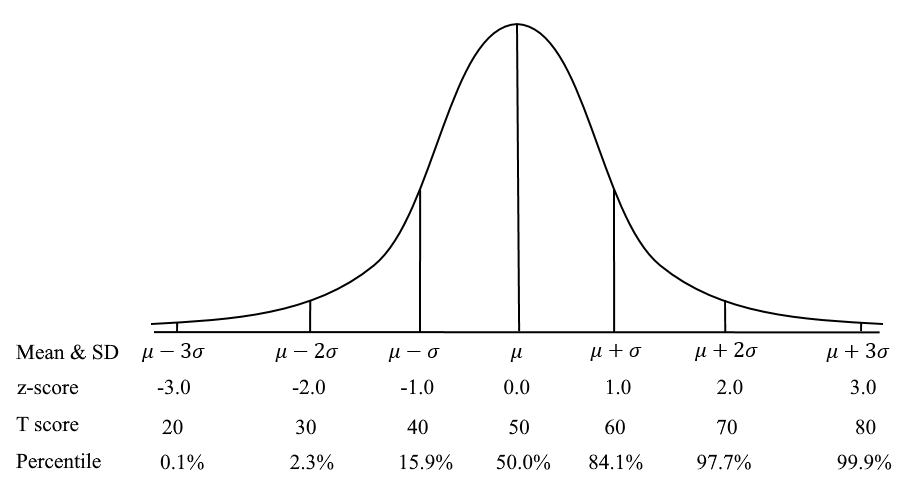
T scores

Advantages of using a z-score

When you standardize the raw data by transforming them into z-scores, you receive the following benefits:

  • Identify outliers
  • Understand where an individual score fits into a distribution
  • Normalize scores for statistical decision-making (e.g., grading on a curve)
  • Calculate probabilities and percentiles using the standard normal distribution
  • Compare scores on different distributions with different means and standard deviations

Example of using a z-score in real life situation

Let’s imagine that there is a set of SAT scores from students, and this data set obeys a normal distribution law with the mean score of  500  and a standard deviation of  100. Suppose we need to find the probability that these SAT scores exceed  650. In order to standardize our data, we have to find the z-score for  650. The z will tell us how many standard deviations away from the mean  650  is.

  • Subtracting the mean from the individual value:

x – 650

μ – 500

x – μ = 650– 500= 150

  • Dividing the obtained difference by the standard deviation:

σ – 100

z = 150 ÷ 100 = 1.5

The z for the value of  650  is  1.5, i.e.  650 is 1.5 standard deviations above the mean in our distribution.

If you look up this z-score on a conversion table, you will see that it says  0.93319.  This means that a score of  650  is at the  93rd  percentile of students.

Additional resources

Khan Academy

Normal Distribution (Wikipedia)

The following two tabs change content below.
Laila Issayeva
My Twitter profileMy LinkedIn profile

Laila Issayeva M.Sc.

Laila Baudinovna Issayeva earned her M.Sc. in Educational Leadership from Nazarbayev University with a focus on School Leadership and Improvement Management. Her undergraduate degree was from Aktobe Regional State University with a major in Mathematics and a minor in Computer Science. Laila is an experienced educator and an educational measurement specialist with expertise in item and test development, setting standards, analyzing, interpreting, and presenting data based on classical test theory and item response theory (IRT). As a professional, Laila is primarily interested in the employment of IRT methodology and artificial intelligence technologies to educational improvement.
/by