Análisis y Estadísticas de Ítems

El análisis de ítems es la evaluación estadística de las preguntas de la prueba para garantizar que sean de buena calidad y corregirlas si no lo son. Este es un paso clave en el ciclo de desarrollo de la prueba; después de que los ítems se han entregado a los examinados (ya sea como piloto o en uso completo), analizamos las estadísticas para determinar si hay problemas que afecten la validez y confiabilidad, como ser demasiado difíciles o sesgados. Esta publicación describirá los conceptos básicos de este proceso. Si desea más detalles e instrucciones sobre el uso del software, también puede consultar nuestros videos tutoriales en nuestro canal de YouTube y descargar nuestro software psicométrico gratuito.

Descargue una copia gratuita de Iteman: software para análisis de ítems

¿Qué es el análisis de ítems?

El análisis de ítems se refiere al proceso de analizar estadísticamente los datos de evaluación para evaluar la calidad y el desempeño de los ítems de la prueba. Este es un paso importante en el ciclo de desarrollo de la prueba, no solo porque ayuda a mejorar la calidad de la prueba, sino porque proporciona documentación para la validez: evidencia de que la prueba funciona bien y que las interpretaciones de las puntuaciones significan lo que usted pretende. Es una de las aplicaciones más comunes de la psicometría, mediante el uso de estadísticas de ítems para marcar, diagnosticar y corregir los ítems de bajo rendimiento en una prueba. Cada ítem que tiene un bajo rendimiento está perjudicando potencialmente a los examinados.

El análisis de ítems se reduce a dos objetivos:

1. Encontrar los ítems que no funcionan bien (dificultad y discriminación, por lo general)
2. Descubrir POR QUÉ esos elementos no funcionan bien, para que podamos determinar si los revisamos o los retiramos

Existen diferentes formas de evaluar el desempeño, como por ejemplo si el ítem es demasiado difícil/fácil, demasiado confuso (no discriminatorio), mal codificado o tal vez incluso sesgado hacia un grupo minoritario.

Además, existen dos paradigmas completamente diferentes para este análisis: la teoría clásica de los pruebas (TCP) y la teoría de respuesta al ítem (TRI). Además de eso, los análisis pueden diferir en función de si el ítem es dicotómico (correcto/incorrecto) o politómico (2 o más puntos).

Debido a las posibles variaciones, el análisis de ítems es un tema complejo. Pero eso ni siquiera entra en la evaluación del desempeño en las pruebas. En esta publicación, cubriremos algunos de los conceptos básicos de cada teoría, a nivel de ítem.

 

Cómo hacer un análisis de ítems

1. Prepare sus datos para el análisis de ítems

La mayoría del software psicométrico utiliza una matriz de persona x elemento. Es decir, un archivo de datos donde los examinados son filas y los elementos son columnas. A veces, es una matriz dispersa donde faltan muchos datos, como en las pruebas lineales sobre la marcha. También deberá proporcionar metadatos al software, como los identificadores de los elementos, las respuestas correctas, los tipos de elementos, etc. El formato para esto variará según el software.

2. Ejecutar datos a través de un software de análisis de ítems

Para implementar el análisis de ítems, debe utilizar un software dedicado diseñado para este propósito. Si utiliza una plataforma de evaluación en línea, le proporcionará resultados para el análisis de ítems, como valores P de distractores y biseriales puntuales (si no, no es una plataforma de evaluación real). En algunos casos, puede utilizar software independiente. CITAS proporciona un enfoque simple basado en hojas de cálculo para ayudarlo a aprender los conceptos básicos, completamente gratis. Aquí se encuentra una captura de pantalla de los resultados de CITAS. Sin embargo, los profesionales necesitarán un nivel superior a este. Iteman  y  Xcalibre  son dos programas de software especialmente diseñados por ASC para este propósito, uno para TCP y otro para TRI.

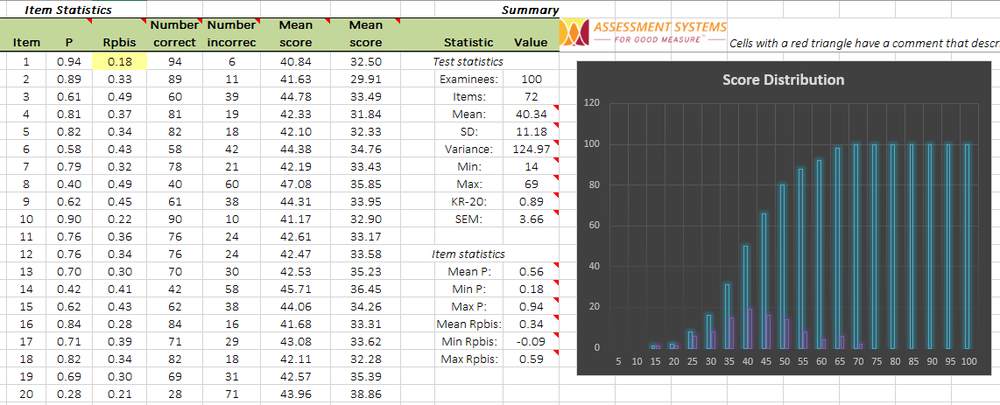
3. Interpretar los resultados del análisis de ítems

El software de análisis de ítems generará tablas de números. A veces, serán tablas feas de estilo ASCII de la década de 1980. A veces, serán hermosos documentos de Word con gráficos y explicaciones. De cualquier manera, debe interpretar las estadísticas para determinar qué ítems tienen problemas y cómo solucionarlos. El resto de este artículo profundizará en eso.

 

Análisis de ítems con la teoría clásica de pruebas

La teoría clásica de tests ofrece un enfoque simple e intuitivo para el análisis de ítems. No utiliza nada más complicado que proporciones, promedios, recuentos y correlaciones. Por este motivo, es útil para exámenes a pequeña escala o para su uso con grupos que no tienen experiencia psicométrica.

Dificultad del ítem: dicotómica

La TCP cuantifica la dificultad del ítem para ítems dicotómicos como la proporción (valor P) de examinados que lo responden correctamente.

Varía de 0,0 a 1,0. Un valor alto significa que el ítem es fácil y un valor bajo significa que el ítem es difícil. No hay reglas estrictas porque la interpretación puede variar ampliamente para diferentes situaciones. Por ejemplo, se esperaría que una prueba realizada al comienzo del año escolar tuviera estadísticas bajas ya que a los estudiantes aún no se les ha enseñado el material. Por otro lado, un examen de certificación profesional, al que alguien ni siquiera puede presentarse a menos que tenga 3 años de experiencia y un título relevante, ¡puede hacer que todos los ítems parezcan fáciles a pesar de que son temas bastante avanzados! A continuación se ofrecen algunas pautas generales:

    0.95-1.0 = Demasiado fácil (no sirve de mucho para diferenciar a los examinados, que es realmente el propósito de la evaluación)

    0.60-0.95 = Típico

    0.40-0.60 = Duro

    <0.40 = Demasiado difícil (considere que una pregunta de opción múltiple de 4 opciones tiene un 25 % de probabilidad de acertar)

Con Iteman, puede establecer límites para marcar automáticamente los ítems. El límite del valor P mínimo representa lo que considera el punto de corte para que un ítem sea demasiado difícil. Para una prueba relativamente fácil, puede especificar 0,50 como mínimo, lo que significa que el 50 % de los examinados han respondido correctamente al ítem.

Para una prueba en la que esperamos que los examinados tengan un desempeño deficiente, el mínimo puede reducirse a 0,4 o incluso a 0,3. El mínimo debe tener en cuenta la posibilidad de adivinar; si el ítem es de opción múltiple con cuatro opciones, existe una probabilidad del 25 % de adivinar la respuesta al azar, por lo que el mínimo probablemente no debería ser 0,20. El valor P máximo representa el punto de corte para lo que considera un ítem demasiado fácil. La consideración principal aquí es que si un ítem es tan fácil que casi todos lo responden correctamente, no está brindando mucha información sobre los examinados. De hecho, los ítems con un P de 0,95 o más suelen tener correlaciones biseriales puntuales muy deficientes.

Tenga en cuenta que debido a que la escala está invertida (un valor más bajo significa una mayor dificultad), esto a veces se conoce como facilidad del ítem.

La media del ítem (politómica)

Se refiere a un ítem que se califica con 2 o más niveles de puntos, como un ensayo calificado con una rúbrica de 0 a 4 puntos o un ítem tipo Likert que se califica en una escala de 1 a 5.

• 1 = Totalmente en desacuerdo
• 2 = En desacuerdo
• 3 = Neutral
• 4 = De acuerdo
• 5 = Totalmente de acuerdo

La media de los ítems es el promedio de las respuestas de los ítems convertidas a valores numéricos de todos los examinados. El rango de la media de los ítems depende de la cantidad de categorías y de si las respuestas de los ítems comienzan en 0. La interpretación de la media de los ítems depende del tipo de ítem (escala de calificación o crédito parcial). Un buen ítem de escala de calificación tendrá una media de ítem cercana a la mitad del máximo, ya que esto significa que, en promedio, los examinados no respaldan categorías cercanas a los extremos del continuo.

Deberá realizar los ajustes necesarios para su propia situación, pero aquí se incluye un ejemplo para el ítem de estilo Likert de 5 puntos.

    1-2 es muy bajo; la gente está bastante en desacuerdo en promedio

    2-3 es bajo a neutral; la gente tiende a estar en desacuerdo en promedio

    3-4 es neutral a alto; la gente tiende a estar de acuerdo en promedio

    4-5 es muy alto; la gente está bastante de acuerdo en promedio

Iteman también proporciona límites de señalización para esta estadística. El límite de la media mínima del ítem representa lo que usted considera el punto de corte para que la media del ítem sea demasiado baja. El límite de la media máxima del ítem representa lo que usted considera el punto de corte para que la media del ítem sea demasiado alta.

Se debe tener en cuenta la cantidad de categorías para los ítems al establecer los límites de los valores mínimos/máximos. Esto es importante ya que todos los ítems de un tipo determinado (por ejemplo, 3 categorías) pueden estar marcados.

Discriminación de ítems: dicotómica

En psicometría, la discriminación es ALGO BUENO, aunque la palabra suele tener una connotación negativa en general. El objetivo de un examen es discriminar entre los examinados; los estudiantes inteligentes deberían obtener una puntuación alta y los no tan inteligentes, una puntuación baja. Si todos obtienen la misma puntuación, no hay discriminación y el examen no tiene sentido. La discriminación de ítems evalúa este concepto.

TCP utiliza la correlación biserial puntual entre ítem y total (Rpbis) como su estadística principal para esto.

La correlación biserial puntual de Pearson (r-pbis) es una medida de la discriminación o fuerza diferenciadora del ítem. Varía de −1,0 a 1,0 y es una correlación de las puntuaciones del ítem y las puntuaciones totales brutas. Si considera una matriz de datos puntuada (ítems de opción múltiple convertidos a datos 0/1), esta sería la correlación entre la columna del ítem y una columna que es la suma de todas las columnas del ítem para cada fila (la puntuación de una persona).

Un buen ítem es capaz de diferenciar entre los examinados de alta y baja capacidad, pero tiene un biserial de puntos más alto, pero rara vez por encima de 0,50. Un biserial de puntos negativo es indicativo de un ítem muy malo porque significa que los examinados de alta capacidad están respondiendo incorrectamente, mientras que los examinados de baja capacidad lo están respondiendo correctamente, lo que por supuesto sería extraño y, por lo tanto, generalmente indica que la respuesta correcta especificada es en realidad incorrecta. Un biserial de puntos de 0,0 no proporciona ninguna diferenciación entre los examinados de baja puntuación y los de alta puntuación, esencialmente “ruido” aleatorio. A continuación se presentan algunas pautas generales sobre la interpretación. Tenga en cuenta que estas suponen un tamaño de muestra decente; si solo tiene una pequeña cantidad de examinados, ¡se marcarán muchas estadísticas de ítems!

    0,20+ = Buen ítem; los examinados más inteligentes tienden a responder el ítem correctamente

    0,10-0,20 = Ítem aceptable; pero probablemente lo revise

    0.0-0.10 = Calidad marginal del ítem; probablemente debería revisarse o reemplazarse

    <0.0 = Ítem terrible; reemplácelo

***Una señal de alerta importante es si la respuesta correcta tiene un Rpbis negativo y un distractor tiene un Rpbis positivo

El límite mínimo de correlación ítem-total representa la discriminación más baja que está dispuesto a aceptar. Este suele ser un número positivo pequeño, como 0,10 o 0,20. Si el tamaño de su muestra es pequeño, es posible que se pueda reducir. El límite máximo de correlación ítem-total es casi siempre 1,0, porque normalmente se desea que el Rpbis sea lo más alto posible.

La correlación biserial también es una medida de la discriminación o fuerza diferenciadora del ítem. Varía de −1,0 a 1,0. La correlación biserial se calcula entre el ítem y la puntuación total como si el ítem fuera una medida continua del rasgo. Dado que la correlación biserial es una estimación de la r de Pearson, será mayor en magnitud absoluta que la correlación biserial puntual correspondiente.

La correlación biserial supone de manera más estricta que la distribución de la puntuación es normal. La correlación biserial no se recomienda para rasgos en los que se sabe que la distribución de puntuaciones no es normal (por ejemplo, patología).

Discriminación de ítems: politómica

La correlación r de Pearson es la correlación producto-momento entre las respuestas de los ítems (como valores numéricos) y la puntuación total. Varía de −1,0 a 1,0. La correlación r indexa la relación lineal entre la puntuación de los ítems y la puntuación total y supone que las respuestas de los ítems forman una variable continua. La correlación r y el Rpbis son equivalentes para un ítem de 2 categorías, por lo que las pautas para la interpretación permanecen inalteradas.

El límite mínimo de correlación ítem-total representa la discriminación más baja que está dispuesto a aceptar. Dado que la correlación r típica (0,5) será mayor que la correlación Rpbis típica (0,3), es posible que desee establecer el límite inferior más alto para una prueba con ítems politómicos (0,2 a 0,3). Si el tamaño de su muestra es pequeño, es posible que se pueda reducir. El límite máximo de correlación ítem-total es casi siempre 1,0, porque normalmente se desea que el Rpbis sea lo más alto posible.

El coeficiente eta es un índice adicional de discriminación calculado mediante un análisis de varianza con la respuesta al ítem como variable independiente y la puntuación total como variable dependiente. El coeficiente eta es la relación entre la suma de cuadrados entre grupos y la suma total de cuadrados y tiene un rango de 0 a 1. El coeficiente eta no supone que las respuestas al ítem sean continuas y tampoco supone una relación lineal entre la respuesta al ítem y la puntuación total.

Como resultado, el coeficiente eta siempre será igual o mayor que la r de Pearson. Tenga en cuenta que se informará la correlación biserial si el ítem tiene solo 2 categorías.

Análisis de claves y distractores

En el caso de muchos tipos de ítems, conviene evaluar las respuestas. Un distractor es una opción incorrecta. Queremos asegurarnos de que no haya más examinados seleccionando un distractor que la clave (valor P) y también de que ningún distractor tenga una mayor discriminación. Esto último significaría que los estudiantes inteligentes están seleccionando la respuesta incorrecta y los no tan inteligentes están seleccionando lo que se supone que es correcto. En algunos casos, el ítem es simplemente malo. En otros, la respuesta simplemente está registrada incorrectamente, tal vez por un error tipográfico. A esto lo llamamos un clave incorrecta del ítem. En ambos casos, queremos marcar el ítem y luego analizar las estadísticas de distractores para averiguar qué está mal.

Ejemplo

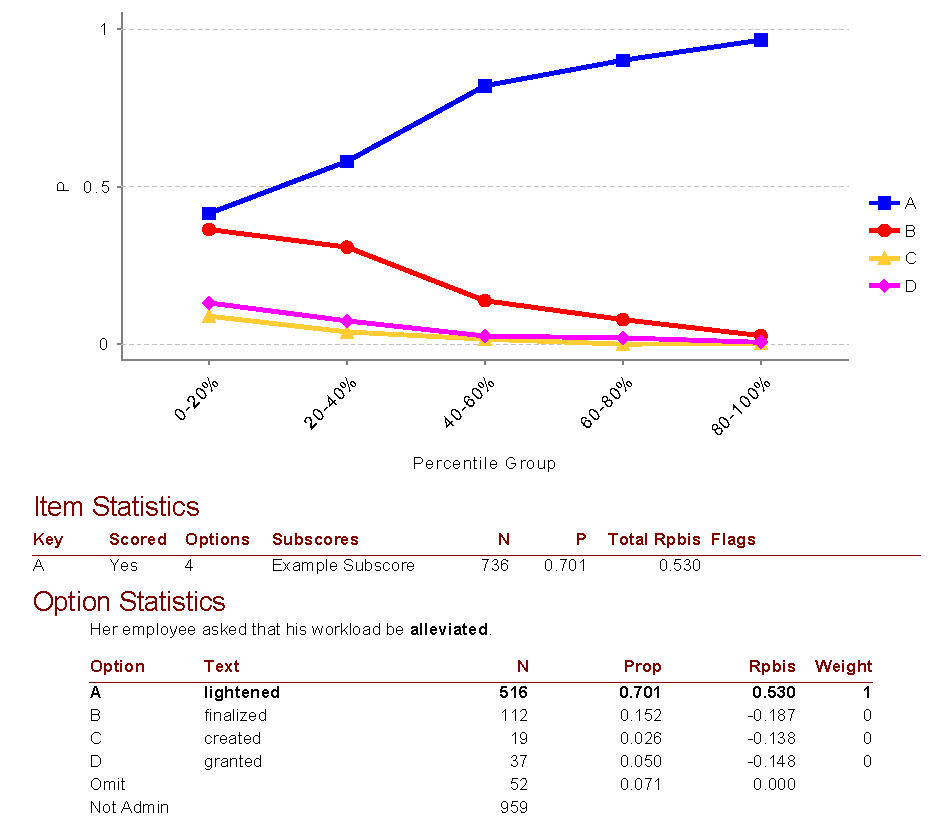
A continuación, se muestra un ejemplo de salida para un elemento de nuestro software  Iteman, que puede descargar de forma gratuita. También puede interesarle este video. Se trata de un elemento con un rendimiento muy bueno. A continuación, se muestran algunas conclusiones clave.

• Este es un ítem de opción múltiple de 4 opciones
• Estaba en una subpuntuación llamada “Subpuntuación de ejemplo”
• Este ítem fue visto por 736 examinados
• El 70 % de los estudiantes lo respondió correctamente, por lo que fue bastante fácil, pero no demasiado fácil
• El Rpbis fue de 0,53, que es extremadamente alto; el ítem es de buena calidad
• La línea para la respuesta correcta en el gráfico de cuantiles tiene una pendiente positiva clara, que refleja la alta calidad de discriminación
• La proporción de examinados que seleccionaron las respuestas incorrectas estuvo bien distribuida, no fue demasiado alta y tuvo valores Rpbis negativos. Esto significa que los distractores son suficientemente incorrectos y no confunden.

 

Análisis de ítems con teoría de respuesta al ítem

La teoría de respuesta al ítem (TRI) es un paradigma muy sofisticado de análisis de ítems y aborda numerosas tareas psicométricas, desde el análisis de ítems hasta la equiparación y las pruebas adaptativas. Requiere tamaños de muestra mucho más grandes que la TCP (100-1000 respuestas por ítem) y una amplia experiencia (normalmente un psicometría con doctorado). La estimación de máxima verosimilitud (MLE) es un concepto clave en la TRI que se utiliza para estimar los parámetros del modelo para una mayor precisión en las evaluaciones.

La TRI no es adecuada para exámenes a pequeña escala, como los cuestionarios en el aula. Sin embargo, se utiliza prácticamente en todos los exámenes “reales” que realizarás en tu vida, desde los exámenes de referencia de K-12 hasta las admisiones universitarias y las certificaciones profesionales.

Si no has utilizado la TRI, te recomiendo que consultes primero esta publicación del blog.

Dificultad de los ítems

La TRI evalúa la dificultad de los ítems dicotómicos como un parámetro b, que es algo así como una puntuación z para el ítem en la curva de campana: 0,0 es promedio, 2,0 es difícil y -2,0 es fácil. (Esto puede diferir un poco con el enfoque de Rasch, que reescala todo). En el caso de los ítems politómicos, hay un parámetro b para cada umbral o paso entre puntos.

Discriminación de ítems

La TRI evalúa la discriminación de ítems por la pendiente de su función de respuesta al ítem, que se denomina parámetro a. A menudo, los valores superiores a 0,80 son buenos y los inferiores a 0,80 son menos efectivos.

Análisis de claves y distractores

En el caso de preguntas politómicas, los múltiples parámetros b proporcionan una evaluación de las diferentes respuestas. En el caso de preguntas dicotómicas, el modelo TRI no distingue entre las respuestas correctas. Por lo tanto, utilizamos el enfoque TCP para el análisis de distractores. Esto sigue siendo extremadamente importante para diagnosticar problemas en preguntas de opción múltiple.

Ejemplo

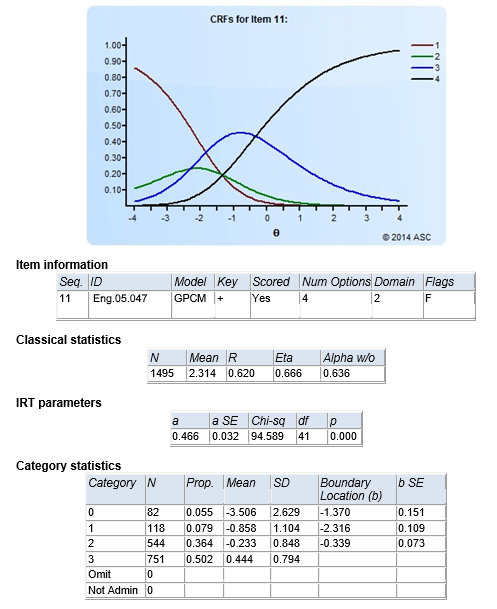
A continuación se muestra un ejemplo de cómo se ve el resultado de un programa de análisis TRI (Xcalibre). También te puede interesar este video.

• Aquí tenemos un ítem politómico, como un ensayo calificado de 0 a 3 puntos
• Está calibrado con el modelo de crédito parcial generalizado
• Tiene una fuerte discriminación clásica (0,62)
• Tiene una mala discriminación TRI (0,466)
• La puntuación bruta promedio fue 2,314 de 3,0, por lo que es bastante fácil
• Hubo una distribución suficiente de las respuestas en los cuatro niveles de puntos
• Los parámetros límite no están en secuencia; este ítem debe revisarse

 

Resumen

Este artículo es una descripción general muy amplia y no hace justicia a la complejidad de la psicometría y el arte de diagnosticar/revisar ítems. Te recomiendo que descargues algún software de análisis de ítems y comiences a explorar tus propios datos.

Para lecturas adicionales, recomiendo algunos de los libros de texto comunes. Para obtener más información sobre cómo escribir/revisar ítems, consulta Haladyna (2004) y trabajos posteriores. Para la teoría de respuesta a los ítems, recomiendo enfáticamente Embretson & Riese (2000).