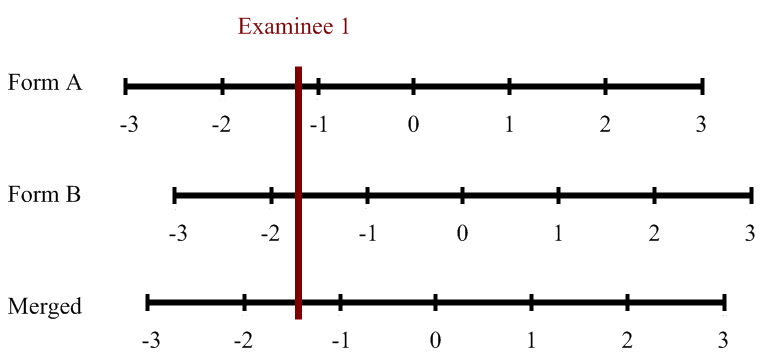
Test Score Equating and Linking
Test equating refers to the issue of defensibly translating scores from one test form to another. That is, if you have an exam where half of students see one set of items while the other half see a different set, how do you know that a score of 70 is the same one both forms? What if one is a bit easier? If you are delivering assessments in conventional linear forms – or piloting a bank for CAT/LOFT – you are likely to utilize more than one test form, and, therefore, are faced with the issue of test equating.
When two test forms have been properly equated, educators can validly interpret performance on one test form as having the same substantive meaning compared to the equated score of the other test form (Ryan & Brockmann, 2009). While the concept is simple, the methodology can be complex, and there is an entire area of psychometric research devoted to this topic. This post will provide an overview of the topic.
Why do we need test linking and equating?
The need is obvious: to adjust for differences in difficulty to ensure that all examinees receive a fair score on a stable scale. Suppose you take Form A and get a score of 72/100 while your friend takes Form B and gets a score of 74/100. Is your friend smarter than you, or did his form happen to have easier questions? What if the passing score on the exam was 73? Well, if the test designers built-in some overlap of items between the forms, we can answer this question empirically.
Suppose the two forms overlap by 50 items, called anchor items or equator items. They are delivered to a large, representative sample. Here are the results.
| Mean score on 50 overlap items | Mean score on 100 total items |
|---|---|
| 30 | 72 |
| 32 | 74 |
Because the mean score on the anchor items was higher, we then think that the Form B group was a little smarter, which led to a higher total score.
Now suppose these are the results:
| Mean score on 50 overlap items | Mean score on 100 total items |
|---|---|
| 32 | 72 |
| 32 | 74 |
Now, we have evidence that the groups are of equal ability. The higher total score on Form B must then be because the unique items on that form are a bit easier.
What is test equating?
According to Ryan and Brockmann (2009), “Equating is a technical procedure or process conducted to establish comparable scores, with equivalent meaning, on different versions of test forms of the same test; it allows them to be used interchangeably.” (p. 8). Thus, successful equating is an important factor in evaluating assessment validity, and, therefore, it often becomes an important topic of discussion within testing programs.
Practice has shown that scores, and tests producing scores, must satisfy very strong requirements to achieve this demanding goal of interchangeability. Equating would not be necessary if test forms were assembled as strictly parallel, meaning that they would have identical psychometric properties. In reality, it is almost impossible to construct multiple test forms that are strictly parallel, and equating is necessary to attune a test construction process.
Dorans, Moses, and Eignor (2010) suggest the following five requirements towards equating of two test forms:
- tests should measure the same construct (e.g. latent trait, skill, ability);
- tests should have the same level of reliability;
- equating transformation for mapping the scores of tests should be the inverse function;
- test results should not depend on the test form an examinee actually takes;
- the equating function used to link the scores of two tests should be the same regardless of the choice of (sub) population from which it is derived.
Detecting item parameter drift (IPD) is crucial for the equating process because it helps in identifying items whose parameters have changed. By addressing IPD, test developers can ensure that the equating process remains valid and reliable.
How do I calculate an equating?
Classical test theory (CTT) methods include linear equating and equipercentile equating as well as several others. Some newer approaches that work well with small samples are Circle-Arc (Livingston & Kim, 2009) and Nominal Weights (Babcock, Albano, & Raymond, 2012). Specific methods for linear equating include Tucker, Levine, and Chained (von Davier & Kong, 2003). Linear equating approaches are conceptually simple and easy to interpret; given the examples above, the equating transformation might be estimated with a slope of 1.01 and an intercept of 1.97, which would directly confirm the hypothesis that one form was about 2 points easier than the other.
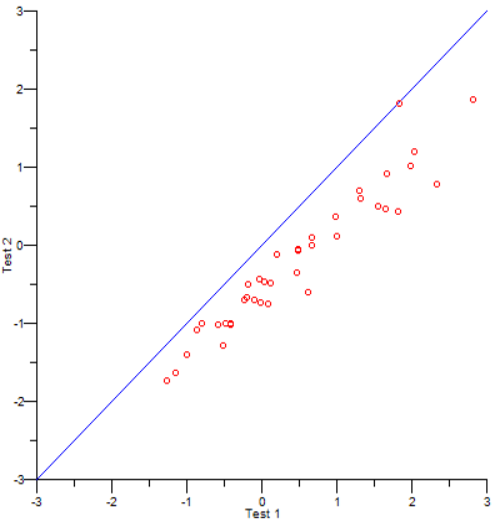
Item response theory (IRT) approaches include equating through common items (equating by applying an equating constant, equating by concurrent or simultaneous calibration, and equating with common items through test characteristic curves), and common person calibration (Ryan & Brockmann, 2009). The common-item approach is quite often used, and specific methods for finding the constants (conversion parameters) include Stocking-Lord, Haebara, Mean/Mean, and Mean/Sigma. Because IRT assumes that two scales on the same construct differ by only a simple linear transformation, all we need to do is find the slope and intercept of that transformation. Those methods do so, and often produce nice looking figures like the one below from the program IRTEQ (Han, 2007). Note that the b parameters do not fall on the identity line, because there was indeed a difference between the groups, and the results clearly find that is the case.
Practitioners can equate forms with CTT or IRT. However, one of the reasons that IRT was invented was that equating with CTT was very weak. Hambleton and Jones (1993) explain that when CTT equating methods are applied, both ability parameter (i.e., observed score) and item parameters (i.e., difficulty and discrimination) are dependent on each other, limiting its utility in practical test development. IRT solves the CTT interdependency problem by combining ability and item parameters in one model. The IRT equating methods are more accurate and stable than the CTT methods (Hambleton & Jones, 1993; Han, Kolen, & Pohlmann, 1997; De Ayala, 2013; Kolen and Brennan, 2014) and provide a solid basis for modern large-scale computer-based tests, such as computerized adaptive tests (Educational Testing Service, 2010; OECD, 2017).
Of course, one of the reasons that CTT is still around in general is that it works much better with smaller samples, and this is also the case for CTT test equating (Babcock, Albano, & Raymond, 2012).
How do I implement test equating?
Test equating is a mathematically complex process, regardless of which method you use. Therefore, it requires special software. Here are some programs to consider.
- CIPE performs both linear and equipercentile equating with classical test theory. It is available from the University of Iowa’s CASMA site, which also includes several other software programs.
- IRTEQ is an easy-to-use program which performs all major methods of IRT Conversion equating. It is available from the University of Massachusetts website, as well as several other good programs.
- There are many R packages for equating and related psychometric topics. This article claims that there are 45 packages for IRT analysis alone!
- If you want to do IRT equating, you need IRT calibration software. We highly recommend Xcalibre since it is easy to use and automatically creates reports in Word for you. If you want to do the calibration approach to IRT equating (both anchor-item and concurrent-calibration), rather than the conversion approach, this is handled directly by IRT software like Xcalibre. For the conversion approach, you need separate software like IRTEQ.
Equating is typically performed by highly trained psychometricians; in many cases, an organization will contract out to a testing company or consultant with the relevant experience. Contact us if you’d like to discuss this.
Does equating happen before or after delivery?
Both. These are called pre-equating and post-equating (Ryan & Brockmann, 2009). Post-equating means the calculation is done after delivery and you have a full data set, for example if a test is delivered twice per year on a single day, we can do it after that day. Pre-equating is more tricky, because you are trying to calculate the equating before a test form has ever been delivered to an examinee; but this is 100% necessary in many situations, especially those with continuous delivery windows.
How do I learn more about test equating?
If you are eager to learn more about the topic of equating, the classic reference is the book by Kolen and Brennan (2004; 2014) that provides the most complete coverage of score equating and linking. There are other resources more readily available on the internet, like this free handbook from CCSSO. If you would like to learn more about IRT, we suggest the books by De Ayala (2008) and Embretson and Reise (2000). A brief intro of IRT equating is available on our website.
Several new ideas of general use in equating, with a focus on kernel equating, were introduced in the book by von Davier, Holland, and Thayer (2004). Holland and Dorans (2006) presented a historical background for test score linking, based on work by Angoff (1971), Flanagan (1951), and Petersen, Kolen, and Hoover (1989). If you look for a straightforward description of the major issues and procedures encountered in practice, then you should turn to Livingston (2004).
Want to learn more? Talk to a Psychometric Consultant!
References
Angoff, W. H. (1971). Scales, norms and equivalent scores. In R. L. Thorndike (Ed.), Educational measurement (2nd ed., pp. 508-600). American Council on Education.
Babcock, B., Albano, A., & Raymond, M. (2012). Nominal Weights Mean Equating: A Method for Very Small Samples. Educational and Psychological Measurement, 72(4), 1-21.
Dorans, N. J., Moses, T. P., & Eignor, D. R. (2010). Principles and practices of test score equating. ETS Research Report Series, 2010(2), i-41.
De Ayala, R. J. (2008). A commentary on historical perspectives on invariant measurement: Guttman, Rasch, and Mokken.
De Ayala, R. J. (2013). Factor analysis with categorical indicators: Item response theory. In Applied quantitative analysis in education and the social sciences (pp. 220-254). Routledge.
Educational Testing Service (2010). Linking TOEFL iBT Scores to IELTS Scores: A Research Report. Educational Testing Service.
Embretson, S. E., & Reise, S. P. (2000). Item response theory for psychologists. Maheah.
Flanagan, J. C. (1951). Units, scores, and norms. In E. F. Lindquist (Ed.), Educational measurement (pp. 695-763). American Council on Education.
Hambleton, R. K., & Jones, R. W. (1993). Comparison of classical test theory and item response theory and their applications to test development. Educational measurement: issues and practice, 12(3), 38-47.
Han, T., Kolen, M., & Pohlmann, J. (1997). A comparison among IRT true-and observed-score equatings and traditional equipercentile equating. Applied Measurement in Education, 10(2), 105-121.
Holland, P. W., & Dorans, N. J. (2006). Linking and equating. In R. L. Brennan (Ed.), Educational measurement (4th ed., pp. 187-220). Praeger.
Kolen, M. J., & Brennan, R. L. (2004). Test equating, linking, and scaling: Methods and practices (2nd ed.). Springer-Verlag.
Kolen, M. J., & Brennan, R. L. (2014). Item response theory methods. In Test Equating, Scaling, and Linking (pp. 171-245). Springer.
Livingston, S. A. (2004). Equating test scores (without IRT). ETS.
Livingston, S. A., & Kim, S. (2009). The Circle‐Arc Method for Equating in Small Samples. Journal of Educational Measurement 46(3): 330-343.
OECD (2017). PISA 2015 Technical Report. OECD Publishing.
Petersen, N. S., Kolen, M. J., & Hoover, H. D. (1989). Scaling, norming and equating. In R. L. Linn (Ed.), Educational measurement (3rd ed., pp. 221-262). Macmillan.
Ryan, J., & Brockmann, F. (2009). A Practitioner’s Introduction to Equating with Primers on Classical Test Theory and Item Response Theory. Council of Chief State School Officers.
von Davier, A. A., Holland, P. W., & Thayer, D. T. (2004). The kernel method of test equating. Springer.
von Davier, A. A., & Kong, N. (2003). A unified approach to linear equating for non-equivalent groups design. Research report 03-31 from Educational Testing Service. https://www.ets.org/Media/Research/pdf/RR-03-31-vonDavier.pdf
Laila Issayeva M.Sc.
Latest posts by Laila Issayeva M.Sc. (see all)
- What is Digital Assessment, aka e-Assessment? - May 18, 2024
- What is a z-score? - November 15, 2023
- Digital Badges - May 29, 2023

