differential item functioning

Differential Item Functioning (DIF)

Nathan Thompson, PhDMarch 9, 2023

Differential item functioning (DIF) is a term in psychometrics for the statistical analysis of assessment data to determine if items are performing in a biased manner against some group of examinees.  This analysis is often complemented by item fit analysis, which ensures that each item aligns appropriately with the theoretical model and functions uniformly across different groups.  Most often, this is based on a demographic variable such as gender, ethnicity, or first language. For example, you might analyze a test to see if items are biased against an ethnic minority, such as Blacks or Hispanics in the USA.  Another organization I have worked with was concerned primarily with Urban vs. Rural students.  In the scientific literature, the majority is called the reference group and the minority is called the focal group.

As you would expect from the name, they are trying to find evidence that an item functions (performs) differently for two groups. However, this is not as simple as one group getting the item incorrect (P value) more often. What if that group also has a lower ability/trait level on average? Therefore, we must analyze the difference in performance conditional on ability.  This means we find examinees at a given level of ability (e.g., 20-30th percentile) and compare the difficulty of the item with minority vs majority examinees.

Mantel-Haenszel analysis of differential item functioning

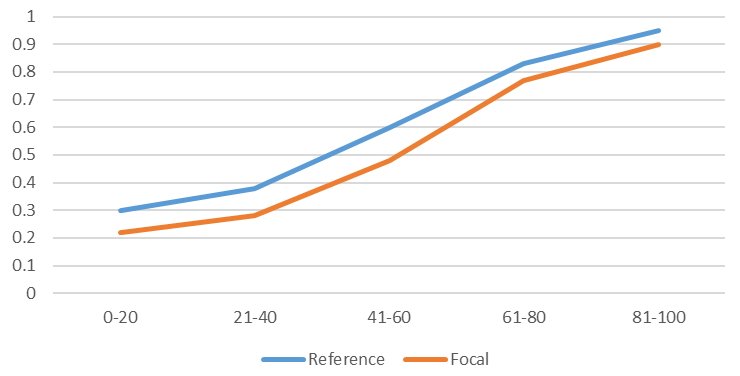
The Mantel-Haenszel approach is a simple yet powerful way to analyze differential item functioning. We simply use the raw classical number-correct score as the indicator of ability, and use it to evaluate group differences conditional on ability. For example, we could split up the sample into fifths (slices of 20%), and for each slice, we evaluate the difference in P value between the groups. An example of this is below, to help visualize how DIF might operate.  Here, there is a notable difference in the probability of getting an item correct, with ability held constant.  The item is biased against the focal group.  In the slice of examinees 41-60th percentile, the reference group has a 60% chance while the focal group (minority) has a 48% chance.

differential item functioning

Crossing and non-crossing DIF

Differential item functioning is sometimes described as crossing or non-crossing DIF. The example above is non-crossing, because the lines do not cross. In this case, there would be a difference in the overall P value between the groups. A case of crossing DIF would see the two lines cross, with potentially no difference in overall P value – which would mean that DIF would go completely unnoticed unless you specifically did a DIF analysis like this.  Hence, it is important to perform DIF analysis; though not for just this reason.

More methods of evaluating differential item functioning

There are, of course, more sophisticated methods of analyzing differential item functioning.  Logistic regression is a commonly used approach.  A sophisticated methodology is Raju’s differential functioning of items and tests (DFIT) approach.

How do I implement DIF?

There are three ways you can implement a DIF analysis.

1. General psychometric software: Well-known software for classical or item response theory analysis will often include an option for DIF. Examples are Iteman, Xcalibre, and IRTPRO (formerly Parscale/Multilog/Bilog).

2. DIF-specific software: While there are not many, there are software programs or R packages that are specific to DIF. An example is DFIT; there used to be a software named that, to do the analysis of the same name.  However, the software is no longer supported but you can use an R package like this.

3. General statistical software or programming environments: For example, if you are a fan of SPSS, you can use it to implement some DIF analyses such as logistic regression.

More resources on differential item functioning

Sage Publishing puts out “little green books” that are useful introductions to many topics.  There is one specifically on differential item functioning.

The following two tabs change content below.
Avatar for Nathan Thompson, PhD
My Twitter profileMy LinkedIn profileMy YouTube channel

Nathan Thompson, PhD

Nathan Thompson earned his PhD in Psychometrics from the University of Minnesota, with a focus on computerized adaptive testing. His undergraduate degree was from Luther College with a triple major of Mathematics, Psychology, and Latin. He is primarily interested in the use of AI and software automation to augment and replace the work done by psychometricians, which has provided extensive experience in software design and programming. Dr. Thompson has published over 100 journal articles and conference presentations, but his favorite remains https://scholarworks.umass.edu/pare/vol16/iss1/1/ .
Avatar for Nathan Thompson, PhD
My Twitter profileMy LinkedIn profileMy YouTube channel

Latest posts by Nathan Thompson, PhD (see all)

/by