¿Qué es el escalamiento vertical en la evaluación?

El escalamiento vertical es el proceso de colocar las puntuaciones de las evaluaciones educativas que miden el mismo dominio de conocimiento pero en diferentes niveles de habilidad en una escala común (Tong y Kolen, 2008). El ejemplo más común es colocar las evaluaciones de Matemáticas o Lenguaje para K-12 en una sola escala para todos los grados. Por ejemplo, puede tener un currículo de matemáticas de grado 4, grado 5, grado 6… en lugar de tratarlos a todos como islas, consideramos todo el recorrido y vinculamos los grados en un solo banco de ítems. Si bien se puede encontrar información general sobre el escalamiento en ¿Qué es el escalamiento de pruebas?, este artículo se centrará específicamente en el escalamiento vertical.

¿Por qué escalamiento vertical?

Una escala vertical es increíblemente importante, ya que permite inferencias sobre el progreso del estudiante de un momento a otro, por ejemplo, de los grados de primaria a secundaria, y puede considerarse como un continuo de desarrollo de los logros académicos del estudiante. En otras palabras, los estudiantes avanzan a lo largo de ese continuo a medida que desarrollan nuevas habilidades, y su puntaje en la escala se altera como resultado (Briggs, 2010).

Esto no solo es importante para los estudiantes individuales, porque podemos hacer un seguimiento del aprendizaje y asignar intervenciones o enriquecimientos apropiados, sino también en un sentido agregado. ¿Qué escuelas están creciendo más que otras? ¿Son mejores ciertos maestros? ¿Quizás haya una diferencia notable entre los métodos de instrucción o los planes de estudio? Aquí, estamos llegando al propósito fundamental de la evaluación; al igual que es necesario tener una báscula de baño para controlar el peso en un régimen de ejercicios, si un gobierno implementa un nuevo método de instrucción de matemáticas, ¿cómo sabe que los estudiantes están aprendiendo de manera más efectiva?

El uso de una escala vertical puede crear un marco interpretativo común para los resultados de las pruebas en todos los grados y, por lo tanto, proporcionar datos importantes que sirvan de base para la enseñanza individual y en el aula. Para que sean válidos y fiables, estos datos deben recopilarse en base a escalas verticales construidas adecuadamente.

Las escalas verticales se pueden comparar con las reglas que miden el crecimiento de los estudiantes en algunas áreas temáticas de un momento de prueba a otro. De manera similar a la altura o el peso, se supone que las capacidades de los estudiantes aumentan con el tiempo. Sin embargo, si tiene una regla de solo 1 metro de largo y está tratando de medir el crecimiento de niños de 3 a 10 años, deberá unir dos reglas.

Construcción de escalas verticales

La construcción de una escala vertical es un proceso complicado que implica tomar decisiones sobre el diseño de la prueba, el diseño de la escala, la metodología de la escala y la configuración de la escala. La interpretación del progreso en una escala vertical depende de la combinación resultante de dichas decisiones de escala (Harris, 2007; Briggs y Weeks, 2009). Una vez que se establece una escala vertical, es necesario mantenerla en diferentes formas y en el tiempo. Según Hoskens et al. (2003), el método elegido para mantener las escalas verticales afecta a la escala resultante y, por lo tanto, es muy importante.

Un modelo de medición que se utiliza para colocar las habilidades de los estudiantes en una escala vertical está representado por la teoría de respuesta al ítem (IRT; Lord, 2012; De Ayala, 2009) o el modelo de Rasch (Rasch, 1960). Este enfoque permite comparaciones directas de los resultados de la evaluación basados ​​en diferentes conjuntos de ítems (Berger et al., 2019). Por lo tanto, se supone que cada estudiante debe trabajar con un grupo seleccionado de ítems que no son similares a los ítems tomados por otros estudiantes, pero aún así sus resultados serán comparables con los de ellos, así como con los suyos propios de otros momentos de evaluación.

La imagen a continuación muestra cómo los resultados de los estudiantes de diferentes grados pueden conceptualizarse mediante una escala vertical común. Suponga que fuera a calibrar los datos de cada grado por separado, pero tiene ítems de anclaje entre los tres grupos. Un análisis de enlace podría sugerir que el Grado 4 está 0,5 logits por encima del Grado 3, y el Grado 5 está 0,7 logits por encima del Grado 4. Puede pensar en las curvas de campana superpuestas como se ve a continuación. Un theta de 0,0 en la escala de Grado 5 es equivalente a 0,7 en la escala de Grado 4, y 1,3 en la escala de Grado 3. Si tiene un enlace fuerte, puede poner los ítems/estudiantes de Grado 3 y Grado 4 en la escala de Grado 5… así como todos los demás grados utilizando el mismo enfoque.

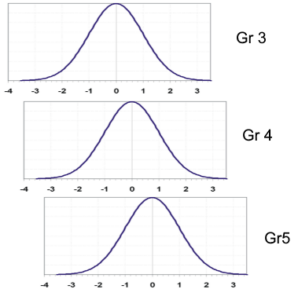
Diseño de pruebas

Kolen y Brennan (2014) nombran tres tipos de diseños de pruebas que apuntan a recopilar datos de respuesta de los estudiantes que deben calibrarse:

• Diseño de grupo equivalente. A los grupos de estudiantes con distribuciones de habilidades presumiblemente comparables dentro de un grado se les asigna aleatoriamente la tarea de responder preguntas relacionadas con su propio grado o con un grado adyacente;
• Diseño de elementos comunes. Utilizar elementos idénticos para estudiantes de grados adyacentes (sin requerir grupos equivalentes) para establecer un vínculo entre dos grados y alinear bloques de elementos superpuestos dentro de un grado, como poner algunos elementos de Grado 5 en la prueba de Grado 6, algunos elementos de Grado 6 en la prueba de Grado 7, etc.;
• Diseño de pruebas de escalamiento. Este tipo es muy similar al diseño de ítems comunes pero, en este caso, los ítems comunes se comparten no solo entre grados adyacentes; hay un bloque de ítems administrado a todos los grados involucrados además de los ítems relacionados con el grado específico.

Desde una perspectiva teórica, el diseño más coherente con una definición de dominio del crecimiento es el diseño de pruebas de escalamiento. El diseño de ítems comunes es el más fácil de implementar en la práctica, pero solo si la administración de los mismos ítems a grados adyacentes es razonable desde una perspectiva de contenido. El diseño de grupos equivalentes requiere procedimientos de administración más complicados dentro de un grado escolar para garantizar muestras con distribuciones de capacidad equivalentes.

Diseño de escala

El procedimiento de escalamiento puede utilizar puntuaciones observadas o puede basarse en IRT. Los procedimientos de diseño de escala más utilizados en configuraciones de escala vertical son los de escala Hieronymus, Thurstone e IRT (Yen, 1986; Yen y Burket, 1997; Tong y Harris, 2004). En todas estas tres metodologías se elige una escala provisional (von Davier et al., 2006).

• Escala de Hieronymus. Este método utiliza una puntuación total de respuestas correctas para las pruebas con puntuación dicotómica o una puntuación total de puntos para los ítems con puntuación politómica (Petersen et al., 1989). La prueba de escala se construye de manera que represente el contenido en un orden creciente en términos del nivel de la prueba, y se administra a una muestra representativa de cada nivel o grado de la prueba. La variabilidad y el crecimiento dentro y entre niveles se establecen en una prueba de escala externa, que es el conjunto especial de ítems comunes.
• Escala de Thurstone. Según Thurstone (1925, 1938), este método crea primero una escala de puntuación provisional y luego normaliza las distribuciones de las variables en cada nivel o grado. Supone que las puntuaciones en una escala subyacente se distribuyen normalmente dentro de cada grupo de interés y, por lo tanto, utiliza un número total de puntuaciones correctas para pruebas con puntuación dicotómica o un número total de puntos de ítems con puntuación politómica para realizar el escalamiento. Por lo tanto, el escalamiento de Thurstone normaliza e iguala linealmente las puntuaciones brutas y, por lo general, se realiza dentro de grupos equivalentes.
• Escala de IRT. Este método de escalamiento considera las interacciones persona-ítem. Teóricamente, el escalamiento IRT se aplica a todos los modelos IRT existentes, incluidos los modelos IRT multidimensionales o los modelos de diagnóstico. En la práctica, solo se utilizan modelos unidimensionales, como los modelos de Rasch y/o de crédito parcial (PCM) o los modelos 3PL (von Davier et al., 2006).

Calibración de datos

Cuando se han tomado todas las decisiones, incluido el diseño de la prueba y el diseño de la escala, y se administran las pruebas a los estudiantes, los ítems deben calibrarse con un software como  Xcalibre  para establecer una escala de medición vertical. Según Eggen y Verhelst (2011), la calibración de ítems dentro del contexto del modelo de Rasch implica el proceso de establecer el ajuste del modelo y estimar el parámetro de dificultad de un ítem basado en los datos de respuesta por medio de procedimientos de estimación de máxima verosimilitud.

Se emplean dos procedimientos, la calibración concurrente y la calibración grado por grado, para vincular los parámetros de dificultad de los ítems basados ​​en la IRT a una escala vertical común en varios grados (Briggs y Weeks, 2009; Kolen y Brennan, 2014). En la calibración concurrente, todos los parámetros de los ítems se estiman en una sola ejecución mediante la vinculación de ítems compartidos por varios grados adyacentes (Wingersky y Lord, 1983). Por el contrario, en la calibración grado por grado, los parámetros de los ítems se estiman por separado para cada grado y luego se transforman en una escala común a través de métodos lineales. El método más preciso para determinar las constantes de enlace minimizando las diferencias entre las curvas características de los elementos de enlace entre las calificaciones es el método de Stocking y Lord (Stocking y Lord, 1983). Esto se logra con software como  IRTEQ.

Resumen del escalamiento vertical

El escalamiento vertical es un tema extremadamente importante en el mundo de la evaluación educativa, especialmente en la educación primaria y secundaria. Como se mencionó anteriormente, esto no solo se debe a que facilita la instrucción para estudiantes individuales, sino que es la base para la información sobre la educación a nivel agregado.

Existen varios enfoques para implementar el escalamiento vertical, pero el enfoque basado en IRT es muy convincente. Una escala IRT vertical permite la representación de la capacidad de los estudiantes en múltiples grados escolares y también la dificultad de los ítems en una amplia gama de dificultades. Además, los ítems y las personas se encuentran en la misma escala latente. Gracias a esta característica, el enfoque IRT admite la selección intencionada de ítems y, por lo tanto, algoritmos para pruebas adaptativas computarizadas (CAT). Estos últimos utilizan estimaciones preliminares de la capacidad para elegir los ítems más apropiados e informativos para cada estudiante individual (Wainer, 2000; van der Linden y Glas, 2010). Por lo tanto, incluso si el conjunto de ítems es de 1000 preguntas que abarcan desde el jardín de infantes hasta el grado 12, puede realizar una sola prueba a cualquier estudiante en el rango y se adaptará a ellos. Mejor aún, puede realizar la misma prueba varias veces al año y, como los estudiantes están aprendiendo, recibirán un conjunto diferente de ítems. Como tal, la CAT con una escala vertical es un enfoque increíblemente adecuado para la evaluación formativa de K-12.

Lectura adicional

Reckase (2010) afirma que la literatura sobre escalamiento vertical es escasa desde la década de 1920 y recomienda algunos estudios de investigación contemporáneos orientados a la práctica:

Paek y Young (2005). Este estudio de investigación abordó los efectos de los valores a priori bayesianos en la estimación de las ubicaciones de los estudiantes en el continuo cuando se utiliza un método de vinculación de parámetros de ítems fijos. Primero, se realizó una calibración dentro del grupo para un nivel de grado; luego, se fijaron los parámetros de los ítems comunes en esa calibración para calibrar el siguiente nivel de grado. Este enfoque obliga a que las estimaciones de los parámetros sean las mismas para los ítems comunes en los niveles de grado adyacentes. Los resultados del estudio mostraron que las distribuciones a priori podrían afectar los resultados y que se deben realizar controles cuidadosos para minimizar los efectos.

Rekase y Li (2007). Este capítulo del libro describe un estudio de simulación de los impactos de la dimensionalidad en el escalamiento vertical. Se emplearon modelos IRT tanto multidimensionales como unidimensionales para simular datos para observar el crecimiento en tres constructos de rendimiento. Los resultados mostraron que el modelo multidimensional recuperó las ganancias mejor que los modelos unidimensionales, pero esas ganancias se subestimaron principalmente debido a la selección de ítems comunes. Esto enfatiza la importancia de usar ítems comunes que cubran todo el contenido evaluado en los niveles de grado adyacentes.

Li (2007). El objetivo de esta tesis doctoral fue identificar si los métodos de IRT multidimensionales podrían usarse para el escalamiento vertical y qué factores podrían afectar los resultados. Este estudio se basó en una simulación diseñada para hacer coincidir los datos de evaluación estatal en Matemáticas. Los resultados mostraron que el uso de enfoques multidimensionales era factible, pero era importante que los ítems comunes incluyeran todas las dimensiones evaluadas en los niveles de grado adyacentes.

Ito, Sykes y Yao (2008). Este estudio comparó la calibración de grupos de grado concurrentes y separados mientras se desarrollaba una escala vertical para nueve grados consecutivos que rastreaban las competencias de los estudiantes en Lectura y Matemáticas. El estudio de investigación utilizó el software BMIRT implementando la estimación de Monte Carlo de cadena de Markov. Los resultados mostraron que las calibraciones simultáneas y por separado de los grupos de grado habían proporcionado resultados diferentes para Matemáticas que para Lectura. Esto, a su vez, confirma que la implementación de la escala vertical es muy difícil y que las combinaciones de decisiones sobre su construcción pueden tener efectos notables en los resultados.

Briggs y Weeks (2009). Este estudio de investigación se basó en datos reales utilizando respuestas a los ítems del Programa de Evaluación de Estudiantes de Colorado. El estudio comparó las escalas verticales basadas en el modelo 3PL con las del modelo Rasch. En general, el modelo 3PL proporcionó escalas verticales con mayores aumentos en el desempeño de un año a otro, pero también mayores aumentos dentro de la variabilidad de grado que la escala basada en el modelo Rasch. Todos los métodos dieron como resultado curvas de crecimiento con menor ganancia junto con un aumento en el nivel de grado, mientras que las desviaciones estándar no fueron muy diferentes en tamaño en diferentes niveles de grado.

Referencias

Berger, S., Verschoor, A. J., Eggen, T. J., & Moser, U. (2019, October). Development and validation of a vertical scale for formative assessment in mathematics. In Frontiers in Education (Vol. 4, p. 103). https://doi.org/10.3389/feduc.2019.00103

Briggs, D. C., & Weeks, J. P. (2009). The impact of vertical scaling decisions on growth interpretations. Educational Measurement: Issues and Practice, 28(4), 3–14.

Briggs, D. C. (2010). Do Vertical Scales Lead to Sensible Growth Interpretations? Evidence from the Field. Online Submission.  https://files.eric.ed.gov/fulltext/ED509922.pdf

De Ayala, R. J. (2009). The Theory and Practice of Item Response Theory. New York: Guilford Publications Incorporated.

Eggen, T. J. H. M., & Verhelst, N. D. (2011). Item calibration in incomplete testing designs. Psicológica 32, 107–132.

Harris, D. J. (2007). Practical issues in vertical scaling. In Linking and aligning scores and scales (pp. 233–251). Springer, New York, NY.

Hoskens, M., Lewis, D. M., & Patz, R. J. (2003). Maintaining vertical scales using a common item design. In annual meeting of the National Council on Measurement in Education, Chicago, IL.

Ito, K., Sykes, R. C., & Yao, L. (2008). Concurrent and separate grade-groups linking procedures for vertical scaling. Applied Measurement in Education, 21(3), 187–206.

Kolen, M. J., & Brennan, R. L. (2014). Item response theory methods. In Test Equating, Scaling, and Linking (pp. 171–245). Springer, New York, NY.

Li, T. (2007). The effect of dimensionality on vertical scaling (Doctoral dissertation, Michigan State University. Department of Counseling, Educational Psychology and Special Education).

Lord, F. M. (2012). Applications of item response theory to practical testing problems. Routledge.

Paek, I., & Young, M. J. (2005). Investigation of student growth recovery in a fixed-item linking procedure with a fixed-person prior distribution for mixed-format test data. Applied Measurement in Education, 18(2), 199–215.

Petersen, N. S., Kolen, M. J., & Hoover, H. D. (1989). Scaling, norming, and equating. In R. L. Linn (Ed.), Educational measurement (3rd ed., pp. 221–262). New York: Macmillan.

Rasch, G. (1960). Probabilistic Models for Some Intelligence and Attainment Tests. Copenhagen: Danmarks Paedagogiske Institut.

Reckase, M. D., & Li, T. (2007). Estimating gain in achievement when content specifications change: a multidimensional item response theory approach. Assessing and modeling cognitive development in school. JAM Press, Maple Grove, MN.

Reckase, M. (2010). Study of best practices for vertical scaling and standard setting with recommendations for FCAT 2.0. Unpublished manuscript. https://www.fldoe.org/core/fileparse.php/5663/urlt/0086369-studybestpracticesverticalscalingstandardsetting.pdf

Stocking, M. L., & Lord, F. M. (1983). Developing a common metric in item response theory. Applied psychological measurement, 7(2), 201–210. doi:10.1177/014662168300700208

Thurstone, L. L. (1925). A method of scaling psychological and educational tests. Journal of educational psychology, 16(7), 433–451.

Thurstone, L. L. (1938). Primary mental abilities (Psychometric monographs No. 1). Chicago: University of Chicago Press.

Tong, Y., & Harris, D. J. (2004, April). The impact of choice of linking and scales on vertical scaling. Paper presented at the annual meeting of the National Council on Measurement in Education, San Diego, CA.

Tong, Y., & Kolen, M. J. (2008). Maintenance of vertical scales. In annual meeting of the National Council on Measurement in Education, New York City.

van der Linden, W. J., & Glas, C. A. W. (eds.). (2010). Elements of Adaptive Testing. New York, NY: Springer.

von Davier, A. A., Carstensen, C. H., & von Davier, M. (2006). Linking competencies in educational settings and measuring growth. ETS Research Report Series, 2006(1), i–36. https://files.eric.ed.gov/fulltext/EJ1111406.pdf

Wainer, H. (Ed.). (2000). Computerized adaptive testing: A Primer, 2nd Edn. Mahwah, NJ: Lawrence Erlbaum Associates.

Wingersky, M. S., & Lord, F. M. (1983). An Investigation of Methods for Reducing Sampling Error in Certain IRT Procedures (ETS Research Reports Series No. RR-83-28-ONR). Princeton, NJ: Educational Testing Service.

Yen, W. M. (1986). The choice of scale for educational measurement: An IRT perspective. Journal of Educational Measurement, 23(4), 299–325.

Yen, W. M., & Burket, G. R. (1997). Comparison of item response theory and Thurstone methods of vertical scaling. Journal of Educational Measurement, 34(4), 293–313.