Monte carlo simulation in adaptive testing
Simulation studies are an essential step in the development of a computerized adaptive test (CAT) that is defensible and meets the needs of your organization or other stakeholders. There are three types of simulations: monte carlo, real data (post hoc), and hybrid.
Monte Carlo simulation is the most general-purpose approach, and the one most often used early in the process of developing a CAT. This is because it requires no actual data, either on test items or examinees – although real data is welcome if available – which makes it extremely useful in evaluating whether CAT is even feasible for your organization before any money is invested in moving forward.
Let’s begin with an overview of how Monte Carlo simulation works before we return to that point.
How a Monte Carlo Simulation works: An Overview
First of all, what do we mean by CAT simulation? Well, a CAT is a test that is administered to students via an algorithm. We can use that same algorithm on imaginary examinees, or real examinees from the past, and simulate how well a CAT performs on them.
Best of all, we can change the specifications of the algorithm to see how it impacts the examinees and the CAT performance.
Each simulation approach requires three things:
- Item parameters from item response theory, though new CAT methods such as diagnostic models are now being developed
- Examinee scores (theta) from item response theory
- A way to determine how an examinee responds to an item if the CAT algorithm says it should be delivered to the examinee.
The monte Carlo simulation approach is defined by how it addresses the third requirement: it generates a response using some sort of mathematical model, while the other two simulation approaches look up actual responses for past examinees (real-data approach) or a mix of the two (hybrid).
The Monte Carlo simulation approach only uses the response generation process. The item parameters can either be from a bank of actual items or generated.
Likewise, the examinee thetas can be from a database of past data, or generated.
How does the response generation process work?
Well, it differs based on the model that is used as the basis for the CAT algorithm. Here, let’s assume that we are using the three-parameter logistic model. Start by supposing we have a fake examinee with a true theta of 0.0. The CAT algorithm looks in the bank and says that we need to administer item #17 as the first item, which has the following item parameters: a=1.0, b=0.0, and c=0.20.
Well, we can simply plug those numbers into the equation for the three-parameter model and obtain the probability that this person would correctly answer this item.
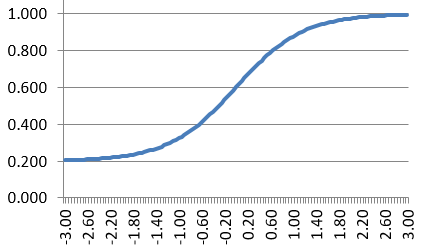
The probability, in this case, is 0.6. The next step is to generate a random number from the set of all real numbers between 0.0 and 1.0. If that number is less than the probability of correct response, the examinee “gets” the item correct. If greater, the examinee gets the item incorrect. Either way, the examinee is scored and the CAT algorithm proceeds.
For every item that comes up to be used, we utilize this same process. Of course, the true theta does not change, but the item parameters are different for each item. Each time, we generate a new random number and compare it to the probability to determine a response of correct or incorrect.
The CAT algorithm proceeds as if a real examinee is on the other side of the computer screen, actually responding to questions, and stops whenever the termination criterion is satisfied. However, the same process can be used to “deliver” linear exams to examinees; instead of the CAT algorithm selecting the next item, we just process sequentially through the test.
A road to research
For a single examinee, this process is not much more than a curiosity. Where it becomes useful is at a large scale aggregate level. Imagine the process above as part of a much larger loop. First, we establish a pool of 200 items pulled from items used in the past by your program. Next, we generate a set of 1,000 examinees by pulling numbers from a random distribution.
Finally, we loop through each examinee and administer a CAT by using the CAT algorithm and generating responses with the Monte Carlo simulation process. We then have extensive data on how the CAT algorithm performed, which can be used to evaluate the algorithm and the item bank. The two most important are the length of the CAT and its accuracy, which are a trade-off in most cases.
So how is this useful for evaluating the feasibility of CAT?
Well, you can evaluate the performance of the CAT algorithm by setting up an experiment to compare different conditions. Suppose you don’t have past items and are not even sure how many items you need? Well, you can create several different fake item banks and administer a CAT to the same set of fake examinees.
Or you might know the item bank to be used, but need to establish that a CAT will outperform the linear tests you currently use. There is a wide range of research questions you can ask, and since all the data is being generated, you can design a study to answer many of them. In fact, one of the greatest problems you might face is that you can get carried away and start creating too many conditions!
How do I actually do a Monte Carlo simulation study?
Fortunately, there is software to do all the work for you. The best option is CATSim, which provides all the options you need in a straightforward user interface (beware, this makes it even easier to get carried away). The advantage of CATSim is that it collates the results for you and presents most of the summary statistics you need without you having to calculate them. For example, it calculates the average test length (number of items used by a variable-length CAT), and the correlation of CAT thetas with true thetas. Other software exists which is useful in generating data sets using Monte Carlo simulation (see SimulCAT), but they do not include this important feature.
Nathan Thompson, PhD
Latest posts by Nathan Thompson, PhD (see all)
- What is an Assessment-Based Certificate? - October 12, 2024
- What is Psychometrics? How does it improve assessment? - October 12, 2024
- What is RIASEC Assessment? - September 29, 2024
