What is Vertical Scaling in Assessment?
Content
Vertical scaling is the process of placing scores from educational assessments that measure the same knowledge domain but at different ability levels onto a common scale (Tong & Kolen, 2008). The most common example is putting Mathematics or Language assessments for K-12 onto a single scale across grades. For example, you might have Grade 4 math curriculum, Grade 5, Grade 6… instead of treating them all as islands, we consider the entire journey and link the grades together in a single item bank. While general information about scaling can be found at What is Test Scaling?, this article will focus specifically on vertical scaling.
Why vertical scaling?
A vertical scale is incredibly important, as enables inferences about student progress from one moment to another, e. g. from elementary to high school grades, and can be considered as a developmental continuum of student academic achievements. In other words, students move along that continuum as they develop new abilities, and their scale score alters as a result (Briggs, 2010).
This is not only important for individual students, because we can track learning and assign appropriate interventions or enrichments, but also in an aggregate sense. Which schools are growing more than others? Are certain teachers better? Perhaps there is a noted difference between instructional methods or curricula? Here, we are coming up to the fundamental purpose of assessment; just like it is necessary to have a bathroom scale to track your weight in a fitness regime, if a governments implements a new Math instructional method, how does it know that students are learning more effectively?
Using a vertical scale can create a common interpretive framework for test results across grades and, therefore, provide important data that inform individual and classroom instruction. To be valid and reliable, these data have to be gathered based on properly constructed vertical scales.
Vertical scales can be compared with rulers that measure student growth in some subject areas from one testing moment to another. Similarly to height or weight, student capabilities are assumed to grow with time. However, if you have a ruler that is only 1 meter long and you are trying to measure growth 3-year-olds to 10-year-olds, you would need to link two rulers together.
Construction of Vertical Scales
Construction of a vertical scale is a complicated process which involves making decisions on test design, scaling design, scaling methodology, and scale setup. Interpretation of progress on a vertical scale depends on the resulting combination of such scaling decisions (Harris, 2007; Briggs & Weeks, 2009). Once a vertical scale is established, it needs to be maintained over different forms and time. According to Hoskens et al. (2003), a method chosen for maintaining vertical scales affects the resulting scale, and, therefore, is very important.
A measurement model that is used to place student abilities on a vertical scale is represented by item response theory (IRT; Lord, 2012; De Ayala, 2009) or the Rasch model (Rasch, 1960). This approach allows direct comparisons of assessment results based on different item sets (Berger et al., 2019). Thus, each student is supposed to work with a selected bunch of items not similar to the items taken by other students, but still his results will be comparable with theirs, as well as with his own ones from other assessment moments.
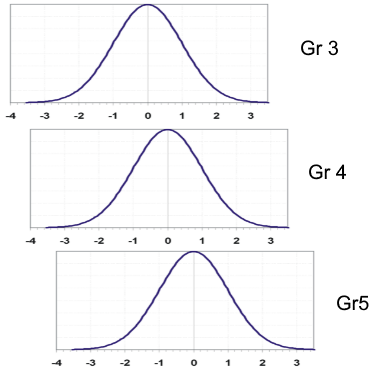
The image below shows how student results from different grades can be conceptualized by a common vertical scale. Suppose you were to calibrate data from each grade separately, but have anchor items between the three groups. A linking analysis might suggest that Grade 4 is 0.5 logits above Grade 3, and Grade 5 is 0.7 logits above Grade 4. You can think of the bell curves overlapped like you see below. A theta of 0.0 on the Grade 5 scale is equivalent to 0.7 on the Grade 4 scale, and 1.3 on the Grade 3 scale. If you have a strong linking, you can put Grade 3 and Grade 4 items/students onto the Grade 5 scale… as well as all other grades using the same approach.
Test design
Kolen and Brennan (2014) name three types of test designs aiming at collecting student response data that need to be calibrated:
- Equivalent group design. Student groups with presumably comparable ability distributions within a grade are randomly assigned to answer items related to their own or an adjacent grade;
- Common item design. Using identical items to students from adjacent grades (not requiring equivalent groups) to establish a link between two grades and to align overlapping item blocks within one grade, such as putting some Grade 5 items on the Grade 6 test, some Grade 6 items on the Grade 7 test, etc.;
- Scaling test design. This type is very similar to common item design but, in this case, common items are shared not only between adjacent grades; there is a block of items administered to all involved grades besides items related to the specific grade.
From a theoretical perspective, the most consistent design with a domain definition of growth is scaling test design. Common item design is the easiest one to implement in practice but only if administering the same items to adjacent grades is reasonable from a content perspective. Equivalent group design requires more complicated administration procedures within one school grade to ensure samples with equivalent ability distributions.
Scaling design
The scaling procedure can use observed scores or it can be IRT-based. The most commonly used scaling design procedures in vertical scale settings are the Hieronymus, Thurstone, and IRT scaling (Yen, 1986; Yen & Burket, 1997; Tong & Harris, 2004). An interim scale is chosen in all these three methodologies (von Davier et al., 2006).
- Hieronymus scaling. This method uses a total number-correct score for dichotomously scored tests or a total number of points for polytomously scored items (Petersen et al., 1989). The scaling test is constructed in a way to represent content in an increasing order in terms of level of testing, and it is administered to a representative sample from each testing level or grade. The within- and between-level variability and growth are set on an external scaling test, which is the special set of common items.
- Thurstone scaling. According to Thurstone (1925, 1938), this method first creates an interim-score-scale and then normalizes distributions of variables at each level or grade. It assumes that scores on an underlying scale are normally distributed within each group of interest and, therefore, makes use of a total number-correct scores for dichotomously scored tests or a total number of points of polytomously scored items to conduct scaling. Thus, Thurstone scaling normalizes and linearly equates raw scores, and it is usually conducted within equivalent groups.
- IRT scaling. This method of scaling considers person-item interactions. Theoretically, IRT scaling is applied for all existing IRT models, including multidimensional IRT models or diagnostic models. In practice, only unidimensional models, such as the Rasch and/or partial credit models (PCM) or the 3PL models, are used (von Davier et al., 2006).
Data calibration
When all decisions are taken, including test design and scaling design, and tests are administered to students, the items need to be calibrated with software like Xcalibre to establish a vertical measurement scale. According to Eggen and Verhelst (2011), item calibration within the context of the Rasch model implies the process of establishing model fit and estimating difficulty parameter of an item based on response data by means of maximum likelihood estimation procedures.
Two procedures, concurrent and grade-by-grade calibration, are employed to link IRT-based item difficulty parameters to a common vertical scale across multiple grades (Briggs & Weeks, 2009; Kolen & Brennan, 2014). Under concurrent calibration, all item parameters are estimated in a single run by means of linking items shared by several adjacent grades (Wingersky & Lord, 1983). In contrast, under grade-by-grade calibration, item parameters are estimated separately for each grade and then transformed into one common scale via linear methods. The most accurate method for determining linking constants by minimizing differences between linking items’ characteristic curves among grades is the Stocking and Lord method (Stocking & Lord, 1983). This is accomplished with software like IRTEQ.
Summary of Vertical Scaling
Vertical scaling is an extremely important topic in the world of educational assessment, especially K-12 education. As mentioned above, this is not only because it facilitates instruction for individual students, but is the basis for information on education at the aggregate level.
There are several approaches to implement vertical scaling, but the IRT-based approach is very compelling. A vertical IRT scale enables representation of student ability across multiple school grades and also item difficulty across a broad range of difficulty. Moreover, items and people are located on the same latent scale. Thanks to this feature, the IRT approach supports purposeful item selection and, therefore, algorithms for computerized adaptive testing (CAT). The latter use preliminary ability estimates for picking the most appropriate and informative items for each individual student (Wainer, 2000; van der Linden & Glas, 2010). Therefore, even if the pool of items is 1,000 questions stretching from kindergarten to Grade 12, you can deliver a single test to any student in the range and it will adapt to them. Even better, you can deliver the same test several times per year, and because students are learning, they will receive a different set of items. As such, CAT with a vertical scale is an incredibly fitting approach for K-12 formative assessment.
Additional Reading
Reckase (2010) states that the literature on vertical scaling is scarce going back to the 1920s, and recommends some contemporary practice-oriented research studies:
Paek and Young (2005). This research study dealt with the effects of Bayesian priors on the estimation of student locations on the continuum when using a fixed item parameter linking method. First, a within group calibration was done for one grade level; then the parameters from the common items in that calibration were fixed to calibrate the next grade level. This approach forces the parameter estimates to be the same for the common items at the adjacent grade levels. The study results showed that the prior distributions could affect the results and that careful checks should be done to minimize the effects.
Reckase and Li (2007). This book chapter depicts a simulation study of the dimensionality impacts on vertical scaling. Both multidimensional and unidimensional IRT models were employed to simulate data to observe growth across three achievement constructs. The results presented that the multidimensional model recovered the gains better than the unidimensional models, but those gains were underestimated mostly due to the common item selection. This emphasizes the importance of using common items that cover all of the content assessed at adjacent grade levels.
Li (2007). The goal of this doctoral dissertation was to identify if multidimensional IRT methods could be used for vertical scaling and what factors might affect the results. This study was based on a simulation designed to match state assessment data in Mathematics. The results showed that using multidimensional approaches was feasible, but it was important that the common items would include all the dimensions assessed at the adjacent grade levels.
Ito, Sykes, and Yao (2008). This study compared concurrent and separate grade group calibration while developing a vertical scale for nine consequent grades tracking student competencies in Reading and Mathematics. The research study used the BMIRT software implementing Markov-chain Monte Carlo estimation. The results showed that concurrent and separate grade group calibrations had provided different results for Mathematics than for Reading. This, in turn, confirms that the implementation of vertical scaling is very challenging, and combinations of decisions about its construction can have noticeable effects on the results.
Briggs and Weeks (2009). This research study was based on real data using item responses from the Colorado Student Assessment Program. The study compared vertical scales based on the 3PL model with those from the Rasch model. In general, the 3PL model provided vertical scales with greater rises in performance from year to year, but also greater increases within grade variability than the scale based on the Rasch model did. All methods resulted in growth curves having less gain along with an increase in grade level, whereas the standard deviations were not much different in size at different grade levels.
References
Berger, S., Verschoor, A. J., Eggen, T. J., & Moser, U. (2019, October). Development and validation of a vertical scale for formative assessment in mathematics. In Frontiers in Education (Vol. 4, p. 103). https://doi.org/10.3389/feduc.2019.00103
Briggs, D. C., & Weeks, J. P. (2009). The impact of vertical scaling decisions on growth interpretations. Educational Measurement: Issues and Practice, 28(4), 3–14.
Briggs, D. C. (2010). Do Vertical Scales Lead to Sensible Growth Interpretations? Evidence from the Field. Online Submission. https://files.eric.ed.gov/fulltext/ED509922.pdf
De Ayala, R. J. (2009). The Theory and Practice of Item Response Theory. New York: Guilford Publications Incorporated.
Eggen, T. J. H. M., & Verhelst, N. D. (2011). Item calibration in incomplete testing designs. Psicológica 32, 107–132.
Harris, D. J. (2007). Practical issues in vertical scaling. In Linking and aligning scores and scales (pp. 233–251). Springer, New York, NY.
Hoskens, M., Lewis, D. M., & Patz, R. J. (2003). Maintaining vertical scales using a common item design. In annual meeting of the National Council on Measurement in Education, Chicago, IL.
Ito, K., Sykes, R. C., & Yao, L. (2008). Concurrent and separate grade-groups linking procedures for vertical scaling. Applied Measurement in Education, 21(3), 187–206.
Kolen, M. J., & Brennan, R. L. (2014). Item response theory methods. In Test Equating, Scaling, and Linking (pp. 171–245). Springer, New York, NY.
Li, T. (2007). The effect of dimensionality on vertical scaling (Doctoral dissertation, Michigan State University. Department of Counseling, Educational Psychology and Special Education).
Lord, F. M. (2012). Applications of item response theory to practical testing problems. Routledge.
Paek, I., & Young, M. J. (2005). Investigation of student growth recovery in a fixed-item linking procedure with a fixed-person prior distribution for mixed-format test data. Applied Measurement in Education, 18(2), 199–215.
Petersen, N. S., Kolen, M. J., & Hoover, H. D. (1989). Scaling, norming, and equating. In R. L. Linn (Ed.), Educational measurement (3rd ed., pp. 221–262). New York: Macmillan.
Rasch, G. (1960). Probabilistic Models for Some Intelligence and Attainment Tests. Copenhagen: Danmarks Paedagogiske Institut.
Reckase, M. D., & Li, T. (2007). Estimating gain in achievement when content specifications change: a multidimensional item response theory approach. Assessing and modeling cognitive development in school. JAM Press, Maple Grove, MN.
Reckase, M. (2010). Study of best practices for vertical scaling and standard setting with recommendations for FCAT 2.0. Unpublished manuscript. https://www.fldoe.org/core/fileparse.php/5663/urlt/0086369-studybestpracticesverticalscalingstandardsetting.pdf
Stocking, M. L., & Lord, F. M. (1983). Developing a common metric in item response theory. Applied psychological measurement, 7(2), 201–210. doi:10.1177/014662168300700208
Thurstone, L. L. (1925). A method of scaling psychological and educational tests. Journal of educational psychology, 16(7), 433–451.
Thurstone, L. L. (1938). Primary mental abilities (Psychometric monographs No. 1). Chicago: University of Chicago Press.
Tong, Y., & Harris, D. J. (2004, April). The impact of choice of linking and scales on vertical scaling. Paper presented at the annual meeting of the National Council on Measurement in Education, San Diego, CA.
Tong, Y., & Kolen, M. J. (2008). Maintenance of vertical scales. In annual meeting of the National Council on Measurement in Education, New York City.
van der Linden, W. J., & Glas, C. A. W. (eds.). (2010). Elements of Adaptive Testing. New York, NY: Springer.
von Davier, A. A., Carstensen, C. H., & von Davier, M. (2006). Linking competencies in educational settings and measuring growth. ETS Research Report Series, 2006(1), i–36. https://files.eric.ed.gov/fulltext/EJ1111406.pdf
Wainer, H. (Ed.). (2000). Computerized adaptive testing: A Primer, 2nd Edn. Mahwah, NJ: Lawrence Erlbaum Associates.
Wingersky, M. S., & Lord, F. M. (1983). An Investigation of Methods for Reducing Sampling Error in Certain IRT Procedures (ETS Research Reports Series No. RR-83-28-ONR). Princeton, NJ: Educational Testing Service.
Yen, W. M. (1986). The choice of scale for educational measurement: An IRT perspective. Journal of Educational Measurement, 23(4), 299–325.
Yen, W. M., & Burket, G. R. (1997). Comparison of item response theory and Thurstone methods of vertical scaling. Journal of Educational Measurement, 34(4), 293–313.
Laila Issayeva M.Sc.
Latest posts by Laila Issayeva M.Sc. (see all)
- What is a z-score? - November 28, 2024
- Confidence Intervals in Assessment and Psychometrics - November 25, 2024
- General Intelligence and Its Role in Assessment and Measurement - November 10, 2024
