What is the Spearman-Brown formula?
The Spearman-Brown formula, also known as the Spearman-Brown Prophecy Formula or Correction, is a method used in evaluating test reliability. It is based on the idea that split-half reliability has better assumptions than coefficient alpha but only estimates reliability for a half-length test, so you need to implement a correction that steps it up to a true estimate for a full-length test.
Looking for software to help you analyze reliability? Download a free copy of Iteman.
Coefficient Alpha vs. Split Half
The most commonly used index of test score reliability is coefficient alpha. However, it’s not the only index on internal consistency. Another common approach is split-half reliability, where you split the test into two halves (first/last, even/odd, or random split) and then correlate scores on each. The reasoning is that if both halves of the test measure the same construct at a similar level of precision and difficulty, then scores on one half should correlate highly with scores on the other half. More information on split-half is found here.
However, split-half reliability provides an inconvenient situation: we are effectively gauging the reliability of half a test. It is a well-known fact that reliability is increased by more items (observations); we can all agree that a 100-item test is more reliable than a 10 item test comprised of similar quality items. So the split half correlation is blatantly underestimating the reliability of the full-length test.
The Spearman-Brown Formula
To adjust for this, psychometricians use the Spearman-Brown prophecy formula. It takes the split half correlation as input and converts it to an estimate of the equivalent level of reliability for the full-length test. While this might sound complex, the actual formula is quite simple.
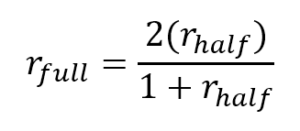
As you can see, the formula takes the split half reliability (rhalf) as input and produces the full-length estimation (rfull) . This can then be interpreted alongside the ubiquitously used coefficient alpha.
While the calculation is quite simple, you still shouldn’t have to do it yourself. Any decent software for classical item analysis will produce it for you. As an example, here is the output of the Reliability Analysis table from our Iteman software for automated reporting and assessment intelligence with CTT. This lists the various split-half estimates alongside the coefficient alpha (and its associated SEM) for the total score as well as the domains, so you can evaluate if there are domains that are producing unusually unreliable scores.
Note: There is an ongoing argument amongst psychometricians whether domain scores are even worthwhile since the assumed unidimensionality of most tests means that the domain scores are less reliable estimates of the total score, but that’s a whole ‘another blog post!
| Score | N Items | Alpha | SEM | Split-Half (Random) | Split-Half (First-Last) | Split-Half (Odd-Even) | S-B Random | S-B First-Last | S-B Odd-Even |
| All items | 50 | 0.805 | 3.058 | 0.660 | 0.537 | 0.668 | 0.795 | 0.699 | 0.801 |
| 1 | 10 | 0.522 | 1.269 | 0.338 | 0.376 | 0.370 | 0.506 | 0.547 | 0.540 |
| 2 | 18 | 0.602 | 1.860 | 0.418 | 0.309 | 0.448 | 0.590 | 0.472 | 0.619 |
| 3 | 12 | 0.605 | 1.496 | 0.449 | 0.417 | 0.383 | 0.620 | 0.588 | 0.553 |
| 4 | 10 | 0.485 | 1.375 | 0.300 | 0.329 | 0.297 | 0.461 | 0.495 | 0.457 |
You can see that, as mentioned earlier, there are 3 ways to do the split in the first place, and Iteman reports all three. It then reports the Spearman-Brown formula for each. These generally align with the results of the alpha estimates, which overall provide a cohesive picture about the structure of the exam and its reliability of scores. As you might expect, domains with more items are slightly more reliable, but not super reliable since they are all less than 20 items.
So, what does this mean in the big scheme of things? Well, in many cases the Spearman-Brown estimates might not differ from the alpha estimates, but it’s still good to know that they do. In the case of high-stakes tests, you want to go through every effort you can to ensure that the scores are highly reliable and precise.
Tell me more!
If you’d like to learn more, here is an article on the topic. Or, contact solutions@assess.com to discuss consulting projects with our Ph.D. psychometricians.
Nathan Thompson, PhD
Latest posts by Nathan Thompson, PhD (see all)
- Psychometrics: Data Science for Assessment - June 5, 2024
- Setting a Cutscore to Item Response Theory - June 2, 2024
- What are technology enhanced items? - May 31, 2024

