
Inter-Rater Reliability vs Agreement
Inter-rater reliability and inter-rater agreement are important concepts in certain psychometric situations. For many assessments, there is never any encounter with raters, but there certainly are plenty of assessments that do. This article will define these two concepts and discuss two psychometric situations where they are important. For a more detailed treatment, I recommend Tinsley and Weiss (1975), which is one of the first articles that I read in grad school.
Inter-Rater Reliability
Inter-rater reliability refers to the consistency between raters, which is slightly different than agreement. Reliability can be quantified by a correlation coefficient. In some cases this is the standard Pearson correlation, but in others it might be tetrachoric or intraclass (Shrout & Fleiss, 1979), especially if there are more than two raters. If raters correlate highly, then they are consistent with each other and would have a high reliability estimate.
Inter-Rater Agreement
Inter-rater agreement looks at how often the two raters give exact the same result. There are different ways to quantify this as well, as discussed below. Perhaps the simplest, in the two-rater case, is to simply calculate the proportion of rows where the two provided the same rating. If there are more than two raters in a case, you will need an index of dispersion amongst their ratings. Standard deviation and mean absolute difference are two examples.
Situation 1: Scoring Essays with Rubrics
If you have an assessment with open-response questions like essays, they need to be scored with a rubric to convert them to numeric scores. In some cases, there is only one rater doing this. You have all had essays graded by a single teacher within a classroom when you were a student. But for larger scale or higher stakes exams, two raters are often used, to provide quality assurance on each other. Moreover, this is often done in an aggregate scale; if you have 10,000 essays to mark, that is a lot for two raters, so instead of two raters rating 10,000 each you might have a team of 20 rating 1,000 each. Regardless, each essay has two ratings, so that inter-rater reliability and agreement can be evaluated. For any given rater, we can easily calculate the correlation of their 1,000 marks with the 1,000 marks from the other rater (even if the other rater rotates between the 19 remaining). Similarly, we can calculate the proportion of times that they provided the same rating or were within 1 point of the other rater.
Situation 2: Modified-Angoff Standard Setting
Another common assessment situation is a modified-Angoff study, which is used to set a cutscore on an exam. Typically, there are 6 to 15 raters that rate each item on its difficulty, on a scale of 0 to 100 in multiple of 5. This makes a more complex situation, since there are not only many more raters per instance (item) but there are many more possible ratings.
To evaluate inter-rater reliability, I typically use the intra-class correlation coefficient, which is:
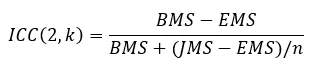
Where BMS is the between items mean-square, EMS is the error mean-square, JMS is the judges mean-square, and n is the number of items. It is like the Pearson correlation used in a two-rater situation, but aggregated across the raters and improved. There are other indices as well, as discussed on Wikipedia.
For inter-rater agreement, I often use the standard deviation (as a very gross index) or quantile “buckets.” See the Angoff Analysis Tool for more information.
Examples of Inter-Rater Reliability vs. Agreement
Consider these three examples with a very simple set of data: two raters scoring 4 students on a 5 point rubric (0 to 5).
Reliability = 1, Agreement = 1
| Student | Rater 1 | Rater 2 |
| 1 | 0 | 0 |
| 2 | 1 | 1 |
| 3 | 2 | 2 |
| 4 | 3 | 3 |
| 5 | 4 | 4 |
Here, the two are always the same, so both reliability and agreement are 1.0.
Reliability = 1, Agreement = 0
| Student | Rater 1 | Rater 2 |
| 1 | 0 | 1 |
| 2 | 1 | 2 |
| 3 | 2 | 3 |
| 4 | 3 | 4 |
| 5 | 4 | 5 |
In this example, Rater 1 is always 1 point lower. They never have the same rating, so agreement is 0.0, but they are completely consistent, so reliability is 1.0.
Reliability = -1, agreement is 0.20 (because they will intersect at middle point)
| Student | Rater 1 | Rater 2 |
| 1 | 0 | 4 |
| 2 | 1 | 3 |
| 3 | 2 | 2 |
| 4 | 3 | 1 |
| 5 | 4 | 0 |
In this example, we have a perfect inverse relationship. The correlation of the two is -1.0, while the agreement is 0.20 (they agree 20% of the time).
Now consider Example 2 with the modified-Angoff situation, with an oversimplification of only two raters.
| Item | Rater 1 | Rater 2 |
| 1 | 80 | 90 |
| 2 | 50 | 60 |
| 3 | 65 | 75 |
| 4 | 85 | 95 |
This is like Example 2 above; one is always 10 points higher, so that there is reliability of 1.0 but agreement of 0. Even though agreement is an abysmal 0, the psychometrician running this workshop would be happy with the results! Of course, real Angoff workshops have more raters and many more items, so this is an overly simplistic example.
References
Tinsley, H.E.A., & Weiss, D.J. (1975). Interrater reliability and agreement of subjective judgments. Journal of Counseling Psychology, 22(4), 358-376.
Shrout, P.E., & Fleiss, J.L. (1979). Intraclass correlations: Uses in assessing rater reliability. Psychological Bulletin, 86(2), 420-428.
Nathan Thompson, PhD
Latest posts by Nathan Thompson, PhD (see all)
- What is an Assessment-Based Certificate? - October 12, 2024
- What is Psychometrics? How does it improve assessment? - October 12, 2024
- What is RIASEC Assessment? - September 29, 2024

