What Is The Standard Error of Measurement?
The standard error of measurement (SEM) is one of the core concepts in psychometrics. One of the primary assumptions of any assessment is that it is accurately and consistently measuring whatever it is we want to measure. We, therefore, need to demonstrate that it is doing so. There are a number of ways of quantifying this, and one of the most common is the SEM.
The SEM can be used in both the classical test theory (CTT) perspective and item response theory (IRT) perspective, though it is defined quite differently in both.
What is measurement error?
We can all agree that assessments are not perfect, from a 4th grade math quiz to a Psych 101 exam at university to a driver’s license test. Suppose you got 80% on an exam today. If we wiped your brain clean and you took the exam tomorrow, what score would you get? Probably a little higher or lower. Psychometricians consider you to have a true score which is what would happen if the test was perfect, you had no interruptions or distractions, and everything else fell into place. But in reality, you of course do not get that score each time. So psychometricians try to estimate the error in your score, and use this in various ways to improve the assessment and how scores are used.
The Standard Error of Measurement in Classical Test Theory
In CTT, it is defined as
SEM = SD*sqrt(1-r),
where SD is the standard deviation of scores for everyone who took the test, and r is the reliability of the test. It is interpreted as the standard deviation of scores that you would find if you had the person take the test over and over, with a fresh mind each time. A confidence interval with this is then interpreted as the band where you would expect the person’s true score on the test to fall.
This has some conceptual disadvantages. For one, it assumes that SEM is the same for all examinees, which is unrealistic. The interpretation focuses only on this single test form rather than the accuracy of measuring someone’s true standing on the trait. Moreover, it does not utilize the examinee’s responses in any way. Lord (1984) suggested a conditional standard error of measurement based on classical test theory, but it focuses on the error of the examinee taking the same test again, rather than the measurement of the true latent value as is done with IRT below.
The classical SEM is reported in Iteman for each subscore, the total score, score on scored items only, and score on pretest items.
Item Response Theory: Conditional Standard Error of Measurement
Early researchers realized that this assumption is unreasonable. Suppose that a test has a lot of easy questions. It will therefore measure low-ability examinees quite well. Imagine that it is a Math placement exam for university, and has a lot of Geometry and Algebra questions at a high school level. It will measure students well who are at that level, but do a very poor job of measuring top students. In an extreme case, let’s say the top 20% of students get every item correct, and there is no way to differentiate them; that defeats the purpose of the test.
The weaknesses of the classical SEM are one of the reasons that IRT was developed. IRT conceptualizes the SEM as a continuous function across the range of student ability, which is an inversion of the test information function (TIF). A test form will have more accuracy – less error – in a range of ability where there are more items or items of higher quality. That is, a test with most items of middle difficulty will produce accurate scores in the middle of the range, but not measure students on the top or bottom very well.
An example of this is shown below. On the right is the conditional standard error of measurement function, and on the left is its inverse, the test information function. Clearly, this test has a lot of items around -1.0 on the theta spectrum, which is around the 15th percentile. Students above 1.0 (85th percentile) are not being measured well.
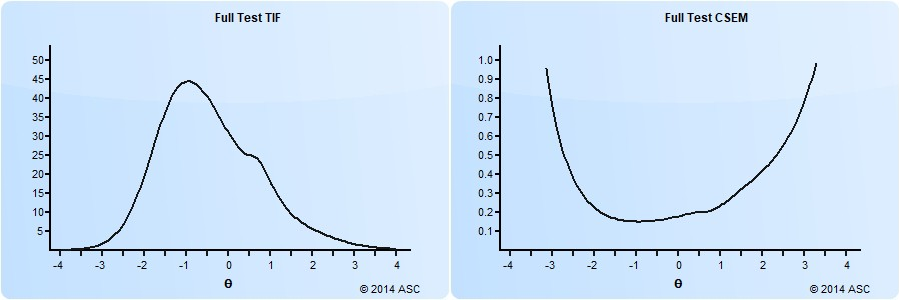
This is actually only the predicted SEM based on all the items in a test/pool. The observed SEM can differ for each examinee based on the items that they answered, and which ones they answered correctly. If you want to calculate the IRT SEM on a test of yours, you need to download Xcalibre and implement a full IRT calibration study.
How is CSEM used?
A useful way to think about conditional standard error of measurement is with confidence intervals. Suppose your score on a test is 0.5 with item response theory. If the CSEM is 0.25 (see above) then we can get a 95% confidence interval by taking plus or minus 2 standard errors. This means that we are 95% certain that your true score lies between 0.0 and 1.0. For a theta of 2.5 with an CSEM of 0.5, that band is then 1.5 to 2.5 – which might seem wide, but remember that is like 94th percentile to 99th percentile.
You will sometimes see scores reported in this manner. I once saw a report on an IQ test that did not give a single score, but instead said “we can expect that 9 times out of 10 that you would score between X and Y.”
There are various ways to use the CSEM and related functions in the design of tests, including the assembly of parallel linear forms and the development of computerized adaptive tests. To learn more about this, I recommend you delve into a book on IRT, such as Embretson and Riese (2000). That’s more than I can cover here.
Nathan Thompson, PhD
Latest posts by Nathan Thompson, PhD (see all)
- What is a T score? - April 15, 2024
- Item Review Workflow for Exam Development - April 8, 2024
- Likert Scale Items - February 9, 2024

