Test Development
Split Half Reliability Index
Split Half Reliability is an internal consistency approach to quantifying the reliability of a test, in the paradigm of classical test theory. Reliability refers to the repeatability or consistency of the test scores; we definitely
What is a Cutscore or Passing Point?
A cutscore or passing point (aka cut-off score and cutoff score as well) is a score on a test that is used to categorize examinees. The most common example of this is pass/fail, which we
Nedelsky Method of Standard Setting
The Nedelsky method is an approach to setting the cutscore of an exam. Originally suggested by Nedelsky (1954), it is an early attempt to implement a quantitative, rigorous procedure to the process of standard setting.
What are Enemy Items?
Enemy items is a psychometric term that refers to two test questions (items) which should not be on the same test form (if linear) seen by a given examinee (if LOFT or adaptive). This can
HR Assessment for Pre-Employment: Approaches and Solutions
HR assessment is a critical part of the HR ecosystem, used to select the best candidates with pre-employment testing, assess training, certify skills, and more. But there is a huge range in quality, as well
Incremental Validity
Incremental validity is a specific aspect of criterion-related validity that refers to what an additional assessment or predictive variable can add to the information provided by existing assessments or variables. It refers to the amount
Public Safety Hiring Practices and Litigation
QUESTION: “What are the costs associated with using validated assessments in public safety hiring?” ANSWER: “Always cheaper than a lawsuit!” It is not uncommon for public safety hiring practices to be called into question. There
Test Score Reliability and Validity
Test score reliability and validity are core concepts in the field of psychometrics and assessment. Both of them refer to the quality of a test, the scores it produces, and how we use those scores.
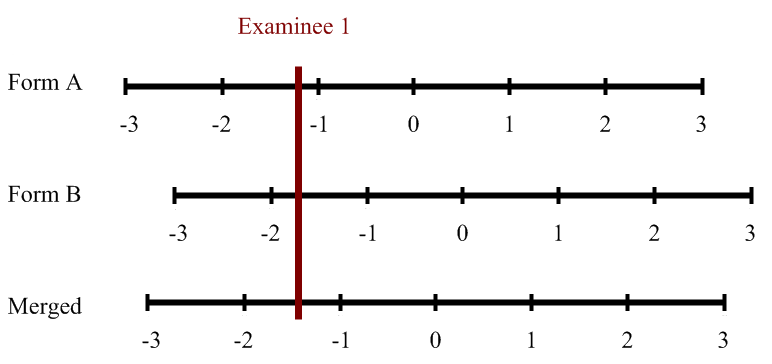
Test Score Equating and Linking
Test equating refers to the issue of defensibly translating scores from one test form to another. That is, if you have an exam where half of students see one set of items while the other
Certification, Certificate, and Licensure Exams – What is the difference?
Certification, Certificate, and Licensure are terms that are used quite frequently to refer to credentialing examinations that someone has to pass to demonstrate skills in a certain profession or topic. They are quite similar, and
The Bookmark Method of Standard Setting
The Bookmark Method of standard setting (Lewis, Mitzel, & Green, 1996) is a scientifically-based approach to setting cutscores on an examination. It allows stakeholders of an assessment to make decisions and classifications about examinees that
What is an Assessment / Test Battery?
A test battery or assessment battery is a set multiple psychometrically-distinct exams delivered in one administration. In some cases, these are various tests that are cobbled together for related purposes, such as a psychologist testing
What is a Psychometric Test?
Psychometric tests are assessments of people to measure psychological attributes such as personality or intelligence. Over the past century, psychometric tests have played an increasingly important part in revolutionizing how we approach important fields such
Three Approaches for IRT Equating
If you are delivering high-stakes tests in linear forms – or piloting a bank for CAT/LOFT – you are faced with the issue of how to equate the forms together. That is, how can we
Paper-and-Pencil Testing: Still Around?
Paper-and-pencil testing used to be the only way to deliver assessments at scale. The introduction of computer-based testing (CBT) in the 1980s was a revelation – higher fidelity item types, immediate scoring & feedback, and
Power of linear on the fly testing
Linear on the fly testing (LOFT) is an approach to assessment delivery that increases test security by limiting item exposure. It tries to balance the advantages of linear testing (e.g., everyone sees the same number
What is a Standard Setting Study?
A standard setting study is a formal process for establishing a performance standard. In the assessment world, there are actually two uses of the word standard - the other one refers to...
What is Item Banking? What are Item Banks?
Item banking refers to the purposeful creation of a database of assessment items to serve as a central repository of all test content, improving efficiency and quality. The term item refers to what many call
