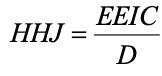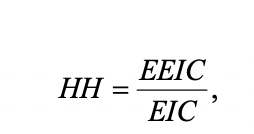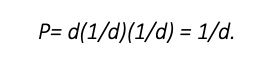One of the core concepts in psychometrics is item difficulty. This refers to the probability that examinees will get the item correct for educational/cognitive assessments or respond in the keyed direction with psychological/survey assessments (more on that later). Difficulty is important for evaluating the characteristics of an item and whether it should continue to be part of the assessment; in many cases, items are deleted if they are too easy or too hard. It also allows us to better understand how the items and test as a whole operate as a measurement instrument, and what they can tell us about examinees.
I’ve heard of “item facility.” Is that similar?
Item difficulty is also called item facility, which is actually a more appropriate name. Why? The P value is a reverse of the concept: a low value indicates high difficulty, and vice versa. If we think of the concept as facility or easiness, then the P value aligns with the concept; a high value means high easiness. Of course, it’s hard to break with tradition, and almost everyone still calls it difficulty. But it might help you here to think of it as “easiness.”
How do we calculate classical item difficulty?
There are two predominant paradigms in psychometrics: classical test theory (CTT) and item response theory (IRT). Here, I will just focus on the simpler approach, CTT.
To calculate classical item difficulty with dichotomous items, you simply count the number of examinees that responded correctly (or in the keyed direction) and divide by the number of respondents. This gets you a proportion, which is like a percentage but is on the scale of 0 to 1 rather than 0 to 100. Therefore, the possible range that you will see reported is 0 to 1. Consider this data set.
| Person | Item1 | Item2 | Item3 | Item4 | Item5 | Item6 | Score |
| 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| 2 | 0 | 0 | 0 | 0 | 1 | 1 | 2 |
| 3 | 0 | 0 | 0 | 1 | 1 | 1 | 3 |
| 4 | 0 | 0 | 1 | 1 | 1 | 1 | 4 |
| 5 | 0 | 1 | 1 | 1 | 1 | 1 | 5 |
| Diff: | 0.00 | 0.20 | 0.40 | 0.60 | 0.80 | 1.00 |
Item6 has a high difficulty index, meaning that it is very easy. Item4 and Item5 are typical items, where the majority of items are responding correctly. Item1 is extremely difficult; no one got it right!
For polytomous items (items with more than one point), classical item difficulty is the mean response value. That is, if we have a 5 point Likert item, and two people respond 4 and two response 5, then the average is 4.5. This, of course, is mathematically equivalent to the P value if the points are 0 and 1 for a no/yes item. An example of this situation is this data set:
| Person | Item1 | Item2 | Item3 | Item4 | Item5 | Item6 | Score |
| 1 | 1 | 1 | 2 | 3 | 4 | 5 | 1 |
| 2 | 1 | 2 | 2 | 4 | 4 | 5 | 2 |
| 3 | 1 | 2 | 3 | 4 | 4 | 5 | 3 |
| 4 | 1 | 2 | 3 | 4 | 4 | 5 | 4 |
| 5 | 1 | 2 | 3 | 5 | 4 | 5 | 5 |
| Diff: | 1.00 | 1.80 | 2.60 | 4.00 | 4.00 | 5.00 |
Note that this is approach to calculating difficulty is sample-dependent. If we had a different sample of people, the statistics could be quite different. This is one of the primary drawbacks to classical test theory. Item response theory tackles that issue with a different paradigm. It also has an index with the right “direction” – high values mean high difficulty with IRT.
If you are working with multiple choice items, remember that while you might have 4 or 5 responses, you are still scoring the items as right/wrong. Therefore, the data ends up being dichotomous 0/1.
Very important final note: this P value is NOT to be confused with p value from the world of hypothesis testing. They have the same name, but otherwise are completely unrelated. For this reason, some psychometricians call it P+ (pronounced “P-plus”), but that hasn’t caught on.
How do I interpret classical item difficulty?
For educational/cognitive assessments, difficulty refers to the probability that examinees will get the item correct. If more examinees get the item correct, it has low difficulty. For psychological/survey type data, difficulty refers to the probability of responding in the keyed direction. That is, if you are assessing Extraversion, and the item is “I like to go to parties” then you are evaluating how many examinees agreed with the statement.
What is unique with survey type data is that it often includes reverse-keying; the same assessment might also have an item that is “I prefer to spend time with books rather than people” and an examinee disagreeing with that statement counts as a point towards the total score.
For the stereotypical educational/knowledge assessment, with 4 or 5 option multiple choice items, we use general guidelines like this for interpretation.
| Range | Interpretation | Notes |
| 0.0-0.3 | Extremely difficult | Examinees are at chance level or even below, so your item might be miskeyed or have other issues |
| 0.3-0.5 | Very difficult | Items in this range will challenge even top examinees, and therefore might elicit complaints, but are typically very strong |
| 0.5-0.7 | Moderately difficult | These items are fairly common, and a little on the tougher side |
| 0.7-0.90 | Moderately easy | These are the most common range of items on most classically built tests; easy enough that examinees rarely complain |
| 0.90-1.0 | Very easy | These items are mastered by most examinees; they are actually too easy to provide much info on examinees though, and can be detrimental to reliability. |
Do I need to calculate this all myself?
No. There is plenty of software to do it for you. If you are new to psychometrics, I recommend CITAS, which is designed to get you up and running quickly but is too simple for advanced situations. If you have large samples or are involved with production-level work, you need Iteman. Sign up for a free account with the button below. If that is you, I also recommend that you look into learning IRT if you have not yet.