Post-training assessment is an integral part of improving the performance and productivity of employees. To gauge the effectiveness of the training, assessments are the go-to solution for many businesses. They ensure transfer and retention of the training knowledge, provide feedback to employees, and can be used for evaluations. At the aggregate level, they help determine opportunities for improvement at the company. Effective test preparation can enhance the accuracy and reliability of these assessments, ensuring that employees are adequately prepared to demonstrate their knowledge and skills.
Benefits Of Post-Training Assessments
Insight On Company Strengths and Weaknesses
Testing gives businesses and organizations insight into the positives and negatives of their training programs. For example, if an organization realizes that certain employees can’t grasp certain concepts, they may decide to modify how they are delivered or eliminate them completely. The employees can also work on their areas of weaknesses after the assessments, hence improving productivity.
Image: The Future Of Assessments: Tech. ed
Helps in Measuring Performance
Unlike traditional testing which is impossible to perform analytics on the assessments, measure performance and high-fidelity, computer-based assessments can quantify initial goals such as call center skills. By measuring performance, businesses can create data-driven roadmaps on how their employees can achieve their best form in terms of performance.
Advocate For Ideas and Concepts That Can Be Integrated Into The Real World
Workers learn every day and sometimes what they learn is not used in driving the business towards attaining its objectives. This can lead to burnout and information overload in employees, which in turn lowers performance and work quality. By using post-training assessments, you can customize tests to help workers attain skills that are only in alignment with your business goals. Implementing digital assessments can streamline this process, making it easier to deploy adaptive testing methods that provide real-time feedback and tailored learning paths. This can be done by using methods such as adaptive testing.
Other Benefits of Cloud-based Testing Include:
- The assessments can be taken from anywhere in the world
- Saves the company a lot of time and resources
- Improved security compared to traditional assessments
- Improved accuracy and reliability
- Scalability and flexibility
- Increases skill and knowledge transfer
Tips To Improve Your Post-Training Assessments
1. Personalized Testing
Most businesses have an array of different training needs. Most employees have different backgrounds and responsibilities in organizations, which is difficult to create effective generalized tests. To achieve the main objectives of your training, it is important to differentiate the assessments. Sales assessments, technical assessments, management assessments, etc. can not be the same. Even in the same department, there could be diversification in terms of skills and responsibilities. One way to achieve personalized testing is by using methods such as Computerized Adaptive Testing. Through the immense power of AI and machine learning, this method gives you the power to create tests that are unique to employees. Not only does personalized testing improve effectiveness in your workforce, but it is also cost-effective, secure, and in alignment with the best Psychometrics practices in the corporate world. It is also important to keep in mind the components of effective assessments when creating personalized tests.
2. Analyzing Assessment Results
Many businesses don’t see the importance of analyzing training assessment results. How do you expect to improve your training programs and assessments if you don’t check the data? This can tell you important things like where the students are weakest and perhaps need more instruction, or if some questions are wonky.
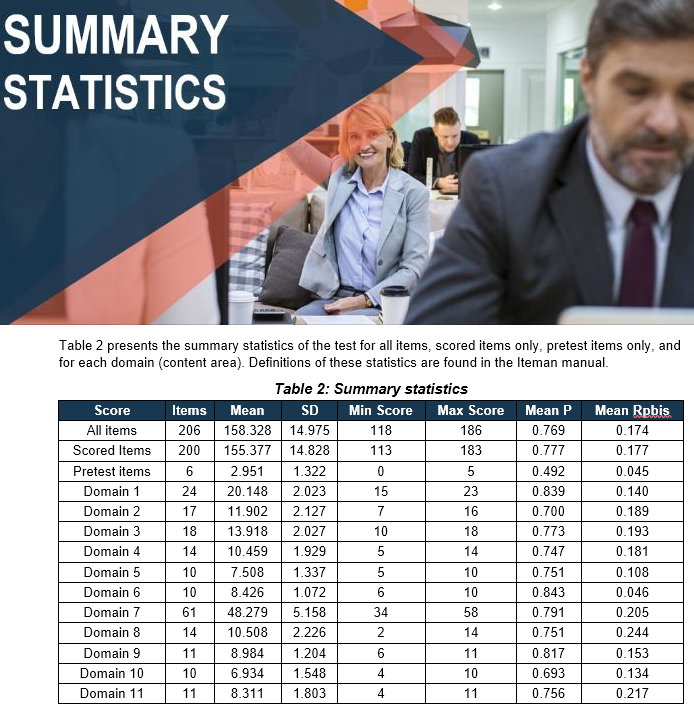
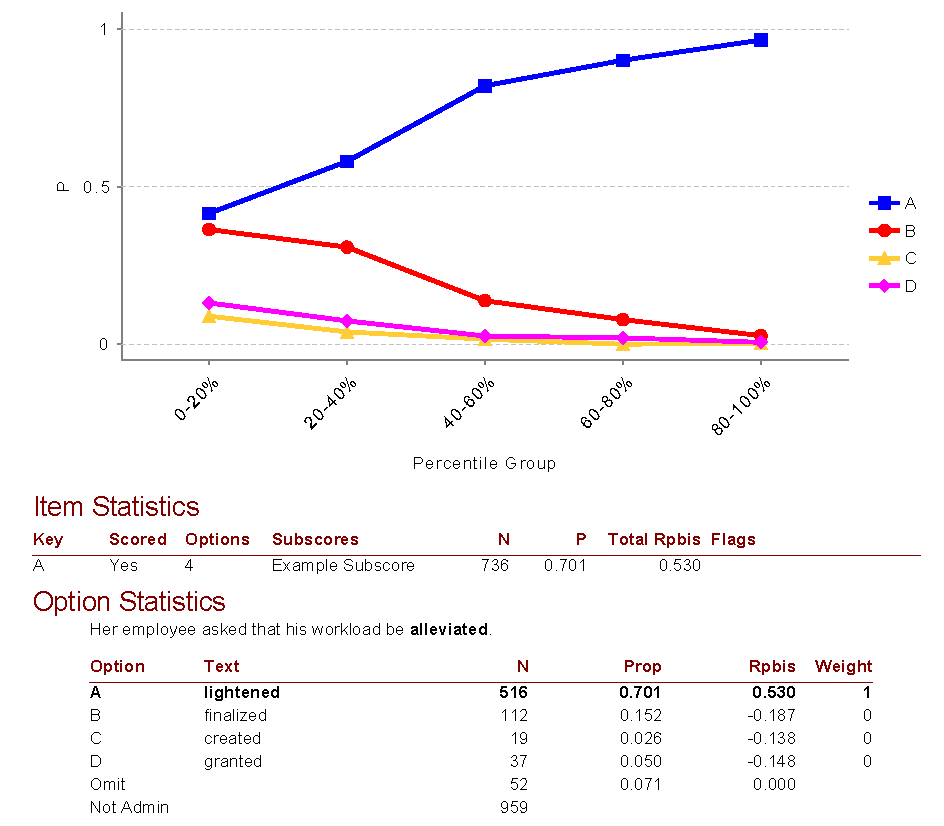
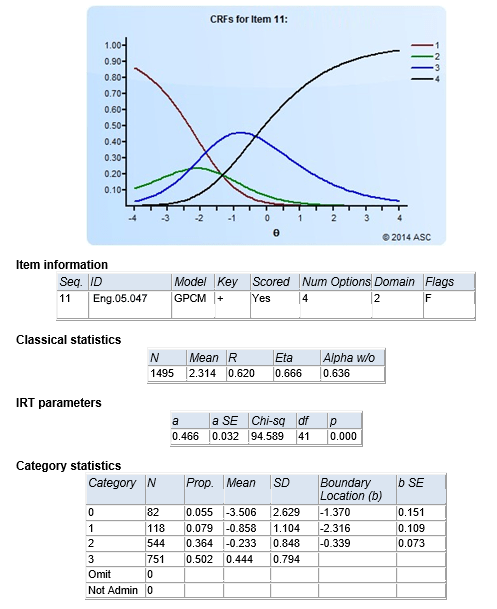
Example of Assessment analysis on Iteman
Analyze assessment results using psychometric analytics software such as Iteman to get important insights such as successful participants, item performance issues, and many others. This provides you with a blueprint to improve your assessments and employee training programs.
3. Integrating Assessment Into Company Culture
Getting the best out of assessment is not about getting it right once, but getting it right over a long period of time. Integrating assessment into company culture is one great way to achieve this. This will make assessment part of the systems and employees will always look forward to improving their skills. You can also use strategies such as gamification to make sure that your employees enjoy the process. It is also critical to give the employees the freedom to provide feedback on the training programs.
4. Diversify Your Assessment Types
One great myth about assessments is that they are limited in terms of questions and problems you can present to your employees. However, this is not true!
By using methods such as item banking, assessment systems are able to provide users with the ability to develop assessments using different question types. Some modern question types include:
- Drag & drop
- Multiple correct
- Embedded audio or video
- Cloze or fill in the blank
- Number lines
- Situational judgment test items
- Counter or timer for performance tests
Diversification of question types improves comprehension in employees and helps them develop skills to approach problems from multiple angles.
5. Choose Your Assessment Tools Carefully
This is among the most important considerations you should make when creating a workforce training assessment strategy. This is because software tools are the core of how your campaigns turn out.
There are many assessment tools available, but choosing one that meets your requirements can be a daunting task. Apart from the key considerations of budget, functionality, etc., there are many other factors to keep in mind before choosing online assessment tools.
To help you choose an assessment tool that will help you in your assessment journey, here are a few things to consider:
Ease-of-use
Most people are new to assessments, and as much as some functionalities can be powerful, they may be overwhelming to candidates and the test development staff. This may make candidates underperform. It is, therefore, important to vet the platform and its functionalities to make sure that they are easy to use.
Functionality
Training assessments are becoming popular and new inventions are being made every day. Does the assessment software have the latest innovations in the industry? Do you get value for your money? Does it support modern psychometrics like item response theory? These are just but a few questions to ask when vetting a platform for functionality.
Assessment Reporting and Visualizations
One major advantage of assessments over traditional ones is that they offer access to instant assessment reporting. You should therefore look for a platform that offers advanced reporting and visualizations in metrics such as performance, question strengths, and many others.
Cheating precautions and Security
When it comes to assessments, there are two concerns when it comes to security. How secure are the assessments? And how secure is the platform? In relation to the tests, the platform should provide precautions and technologies such as Lockdown browser against cheating. They should also have measures in place to make sure that user data is secure.
Reliable Support System
This is one consideration that many businesses don’t keep in mind, and end up regretting in the long run. Which channels does the corporate training assessment platform use to provide its users with support? Do they have resources such as whitepapers and documentation in case you need them? How fast is their support? These are questions you should ask before selecting a platform to take care of your assessment needs.
Scalability
A good testing vendor should be able to provide you with resources should your needs go beyond expectation. This includes delivery volume – server scalability – but also being able to manage more item authors, more assessments, more examinees, and greater psychometric rigor.
Final Thoughts
Adopting effective post-training assessments can be daunting tasks with a lot of forces at play, and we hope these tips will help you get the best out of your assessments.
Do you want to integrate smarter assessments into your corporate environment or any industry but feel overwhelmed by the process? Feel free to contact an experienced team of professionals to help you create an assessment strategy that helps you achieve your long-term goals and objectives.
You can also sign up to get free access to our online assessment suite including 60 item types, IRT, adaptive testing, and so much more functionality!