Test Development Archives

What is a Standard Setting Study?

Nathan Thompson, PhDMay 21, 2021

A standard setting study is a formal, quantitative process for establishing a performance standard on an exam, such as what score is “proficient” or “passing.” This is typically manifested as a cutscore which is then used for making decisions about people: hire them, pass them, accept them into university, etc. Because it is used for such important decisions, a lot of work goes into standard setting, using methods based on scientific research.

What is NOT standard setting?

In the assessment world, there are actually three uses of the word standard:

A formal definition of the content that is being tested, such as the Common Core State Standards in the USA.
A formalized process for delivering exams, as seen in the phrase “standardized testing.”
A benchmark for performance, like we are discussing here.

For this reason, I prefer the term cutscore study, but the phrase standard setting is used more often.

How is a standard setting study used?

As part of a comprehensive test development cycle, after item authoring, item review, and test form assembly, a cutscore or passing score will often be set to determine what level of performance qualified as “pass” or a similar classification. This cannot be done arbitrarily, such as setting it at 70% because that’s what you saw when you were in school. That is a legal landmine! To be legally defensible and eligible for Accreditation of a Certification Program, it must be done using one of several standard-setting approaches from the psychometric literature. So, if your organization is classifying examinees into Pass/Fail, Hire/NotHire, Basic/Proficient/Advanced, or any other groups, you most likely need a standard setting study. This is NOT limited to certification, although it is often discussed in that pass/fail context.

What are some methods of a standard setting study?

There have been many methods suggested in the scientific literature of psychometrics. They are often delineated into examinee-centered and item-centered approaches. Angoff and Bookmark are designed around evaluating items, while Contrasting Groups and Borderline Groups are designed around evaluating the distributions of actual examinee scores. The Bookmark approach is sort of both types, however, because it uses examinee performance on the items as the object of interest. You may also be interested in reading this introductory post on setting a cutscore using item response theory.

Angoff

In an Angoff study, a panel of subject matter experts rates each item, estimating the percentage of minimally competent candidates that would answer each item correctly. If we take the average of all raters, this then translates into the average percentage-correct score that the raters expect from a minimally competent candidate – a very compelling argument for a cutscore to pass competent examinees! It is often done in tandem with the Beuk Compromise. The Angoff method does not require actual examinee data, though the Beuk does.

Bookmark

The bookmark method orders the items in a test form in ascending difficulty, and a panel of experts reads through and places a “bookmark” in the book where they think a cutscore should be. This process requires a sufficient amount of real data to calibrate item difficulty accurately, typically using item response theory, which necessitates data from several hundred examinees. Additionally, the method ensures that the cutscore is both valid and reliable, reflecting the true proficiency needed for the test.

Contrasting Groups

With the contrasting groups approach, candidates are sorted into Pass and Fail groups based on their performance on a different exam or some other unrelated standard. We can then compare the score distributions on our exam for the two separate groups, and pick a cutscore that best differentiates Pass vs Fail on the other standard. An example of this is below. If using data from another exam, a sample of at least 50 candidates is obviously needed, since you are evaluating distributions.

Borderline Group

The Borderline Group method is similar to the Contrasting Groups method, but it defines a borderline group using alternative information, such as biodata, and evaluates the scores of this group. This method involves selecting individuals who are deemed to be on the threshold of passing or failing based on external criteria. These criteria might include previous performance data, demographic information, or other relevant biodata. The scores from this borderline group are then analyzed to determine the cutscore. This approach helps in refining the accuracy of the cutscore by incorporating more nuanced and contextual information about the test-takers.

Hofstee

The Hofstee approach is often used as a reality check for the modified-Angoff method but can also stand alone as a method for setting cutscores. It involves only a few estimates from a panel of SMEs. Specifically, the SMEs provide estimates for the minimum and maximum acceptable failure rates and the minimum and maximum acceptable scores. This data is then plotted to determine a compromise cutscore that balances these criteria. The simplicity and practicality of the Hofstee approach make it a valuable tool in various testing scenarios, ensuring the cutscore is both realistic and justifiable.

Ebel

The Ebel approach categorizes test items by both their importance and difficulty level. This method involves a panel of experts who rate each item on these two dimensions, creating a matrix that helps in determining the cutscore. Despite its thorough and structured approach, the Ebel method is considered very old and has largely fallen out of use in modern testing practices. Advances in psychometric techniques and the development of more efficient and accurate methods, such as item response theory, have led to the Ebel approach being replaced by more contemporary standard-setting techniques.

How to choose an approach?

There is often no specifically correct answer. In fact, guidelines like NCCA do not lay out which method to use, they just tell you to use an appropriate method.

There are several considerations. Perhaps the most important is whether you have existing data. The Bookmark, Contrasting Groups, and Borderline Group approaches all assume that we have data from a test already delivered, which we can analyze with the perspective of the latent standard. The Angoff and Hofstee approaches, in contrast, can be done before a test is ever delivered. This is arguably less defensible, but is a huge practical advantage.

The choice also depends on whether you can easily recruit a panel of subject matter experts, as that is required for Angoff and Bookmark. The Contrasting Groups method assumes we have a gold standard, which is rare.

How can I implement a standard setting study?

If your organization has an in-house psychometrician, they can usually do this. If, for example, you are a board of experts in a profession but lack experience in psychometrics, you need to hire a firm. We can perform such work for you – contact us to learn more.

May 21, 2021/by Nathan Thompson, PhD

What is Item Banking? What are Item Banks?

AdminApril 12, 2021

Item banking refers to the purposeful creation of a database of assessment items to serve as a central repository of all test content, improving efficiency and quality. The term item refers to what many call questions; though their content need not be restricted as such and can include problems to solve or situations to evaluate in addition to straightforward questions. Regular item review is essential to ensure that each item meets content standards, is fair, and is free from bias, thereby maintaining the integrity and accuracy of the item bank. As a critical foundation to the test development cycle, item banking is the foundation for the development of valid, reliable content and defensible test forms.

Automated item banking systems, such as Assess.ai or FastTest, result in significantly reduced administrative time for developing/reviewing items and assembling/publishing tests, while producing exams that have greater reliability and validity. Contact us to request a free account.

Request demo account

What is Item Banking?

While there are no absolute standards in creating and managing item banks, best practice guidelines are emerging. Here are the essentials your should be looking for:

Items are reusable objects; when selecting an item banking platform it is important to ensure that items can be used more than once; ideally, item performance should be tracked not only within a test form but across test forms as well.

Item history and usage are tracked; the usage of a given item, whether it is actively on a test form or dormant waiting to be assigned, should be easily accessible for test developers to assess, as the over-exposure of items can reduce the validity of a test form. As you deliver your items, their content is exposed to examinees. Upon exposure to many examinees, items can then be flagged for retirement or revision to reduce cheating or teaching to the test.

Items can be sorted; as test developers select items for a test form, it is imperative that they can sort items based on their content area or other categorization methods, so as to select a sample of items that is representative of the full breadth of constructs we intend to measure.

Item versions are tracked; as items appear on test forms, their content may be revised for clarity. Any such changes should be tracked and versions of the same item should have some link between them so that we can easily review the performance of earlier versions in conjunction with current versions.

Review process workflow is tracked; as items are revised and versioned, it is imperative that the changes in content and the users who made these changes are tracked. In post-test assessment, there may be a need for further clarification, and the ability to pinpoint who took part in reviewing an item and expedite that process.

Metadata is recorded; any relevant information about an item should be recorded and stored with the item. The most common applications for metadata that we see are author, source, description, content area, depth of knowledge, item response theory parameters, and classical test theory statistics, but there are likely many data points specific to your organization that is worth storing.

Managing an Item Bank

Names are important. As you create or import your item banks it is important to identify each item with a unique, but recognizable name. Naming conventions should reflect your bank’s structure and should include numbers with leading zeros to support true numerical sorting. You might want to also add additional pieces of information. If importing, the system should be smart enough to recognize duplicates.

Search and filter. The system should also have a reliable sorting mechanism.

Prepare for the Future: Store Extensive Metadata

Metadata is valuable. As you create items, take the time to record simple metadata like author and source. Having this information can prove very useful once the original item writer has moved to another department, or left the organization. Later in your test development life cycle, as you deliver items, you have the ability to aggregate and record item statistics. Values like discrimination and difficulty are fundamental to creating better tests, driving reliability, and validity.

Statistics are used in the assembly of test forms while classical statistics can be used to estimate mean, standard deviation, reliability, standard error, and pass rate.

Item response theory parameters can come in handy when calculating test information and standard error functions. Data from both psychometric theories can be used to pre-equate multiple forms.

In the event that your organization decides to publish an adaptive test, utilizing computerized adaptive testing delivery, item parameters for each item will be essential. This is because they are used for intelligent selection of items and scoring examinees. Additionally, in the event that the integrity of your test or scoring mechanism is ever challenged, documentation of validity is essential to defensibility and the storage of metadata is one such vital piece of documentation.

Increase Content Quality: Track Workflow

Utilize a review workflow to increase quality. Using a standardized review process will ensure that all items are vetted in a similar matter. Have a step in the process for grammar, spelling, and syntax review, as well as content review by a subject matter expert. As an item progresses through the workflow, its development should be tracked, as workflow results also serve as validity documentation.

Accept comments and suggestions from a variety of sources. It is not uncommon for each item reviewer to view an item through their distinctive lens. Having a diverse group of item reviewers stands to benefit your test-takers, as they are likely to be diverse as well!

Keep Your Items Organized: Categorize Them

Identify items by content area. Creating a content hierarchy can also help you to organize your item bank and ensure that your test covers the relevant topics. Most often, we see content areas defined first by an analysis of the construct(s) being tested. In the event of a high school science test, this may include the evaluation of the content taught in class. A high-stakes certification exam, almost always includes a job-task analysis. Both methods produce what is called a test blueprint, indicating how important various content areas are to the demonstration of knowledge in the areas being assessed.

Once content areas are defined, we can assign items to levels or categories based on their content. As you are developing your test, and invariably referring back to your test blueprint, you can use this categorization to determine which items from each content area to select.

The Benefits of Item Banking

There is no doubt that item banking is a key aspect of developing and maintaining quality assessments. Utilizing best practices, and caring for your items throughout the test development life cycle, will pay great dividends as it increases the reliability, validity, and defensibility of your assessment. Moreover, good item banking will make the job easier and more efficient thus reducing the cost of item development and test publishing.

Ready to Improve assessment quality through item banking?

Visit our Contact Us page, where you can request a demonstration or a free account (up to 500 items). I also recommend you watch this tutorial video.

April 12, 2021/by Admin

Item Analysis and Statistics

Nathan Thompson, PhDMarch 31, 2021

Item analysis is the statistical evaluation of test questions to ensure they are good quality, and fix them if they are not. This is a key step in the test development cycle; after items have been delivered to examinees (either as a pilot, or in full usage), we analyze the statistics to determine if there are issues which affect validity and reliability, such as being too difficult or biased. This post will describe the basics of this process. If you’d like further detail and instructions on using software, you can also you can also check out our tutorial videos on our YouTube channel and download our free psychometric software.

Download a free copy of Iteman: Software for Item Analysis

What is Item Analysis?

Item analysis refers to the process of statistically analyzing assessment data to evaluate the quality and performance of your test items. This is an important step in the test development cycle, not only because it helps improve the quality of your test, but because it provides documentation for validity: evidence that your test performs well and score interpretations mean what you intend. It is one of the most common applications of psychometrics, by using item statistics to flag, diagnose, and fix the poorly performing items on a test. Every item that is poorly performing is potentially hurting the examinees.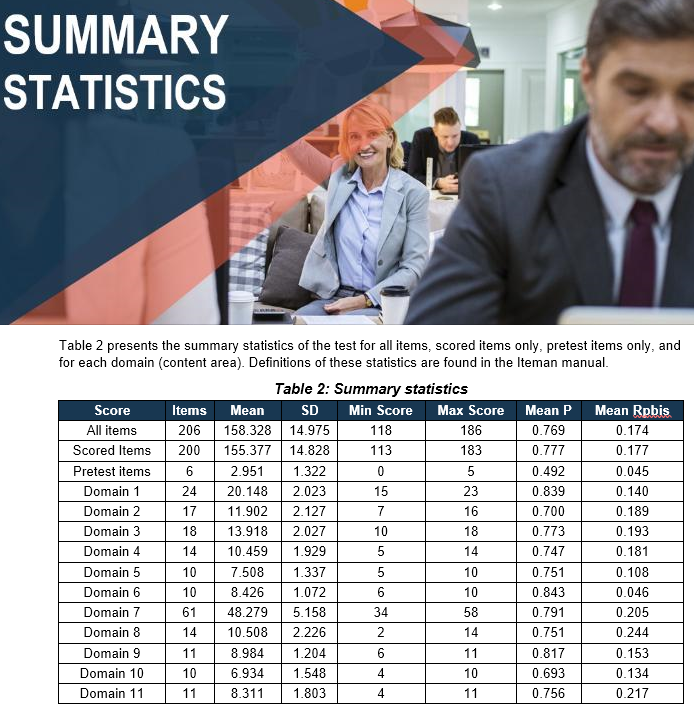

Item analysis boils down to two goals:

Find the items that are not performing well (difficulty and discrimination, usually)
Figure out WHY those items are not performing well, so we can determine whether to revise or retire them

There are different ways to evaluate performance, such as whether the item is too difficult/easy, too confusing (not discriminating), miskeyed, or perhaps even biased to a minority group.

Moreover, there are two completely different paradigms for this analysis: classical test theory (CTT) and item response theory (IRT). On top of that, the analyses can differ based on whether the item is dichotomous (right/wrong) or polytomous (2 or more points).

Because of the possible variations, item analysis complex topic. But, that doesn’t even get into the evaluation of test performance. In this post, we’ll cover some of the basics for each theory, at the item level.

How to do Item Analysis

1. Prepare your data for item analysis

Most psychometric software utilizes a person x item matrix. That is, a data file where examinees are rows and items are columns. Sometimes, it is a sparse matrix where is a lot of missing data, like linear on the fly testing. You will also need to provide metadata to the software, such as your Item IDs, correct answers, item types, etc. The format for this will differ by software.

2. Run data through item analysis software

To implement item analysis, you should utilize dedicated software designed for this purpose. If you utilize an online assessment platform, it will provide you output for item analysis, such as distractor P values and point-biserials (if not, it isn’t a real assessment platform). In some cases, you might utilize standalone software. CITAS provides a simple spreadsheet-based approach to help you learn the basics, completely for free. A screenshot of the CITAS output is here. However, professionals will need a level above this. Iteman and Xcalibre are two specially-designed software programs from ASC for this purpose, one for CTT and one for IRT.

3. Interpret results of item analysis

Item analysis software will produce tables of numbers. Sometimes, these will be ugly ASCII-style tables from the 1980s. Sometimes, they will be beautiful Word docs with graphs and explanations. Either way, you need to interpret the statistics to determine which items have problems and how to fix them. The rest of this article will delve into that.

Item Analysis with Classical Test Theory

Classical Test Theory provides a simple and intuitive approach to item analysis. It utilizes nothing more complicated than proportions, averages, counts, and correlations. For this reason, it is useful for small-scale exams or use with groups that do not have psychometric expertise.

Item Difficulty: Dichotomous

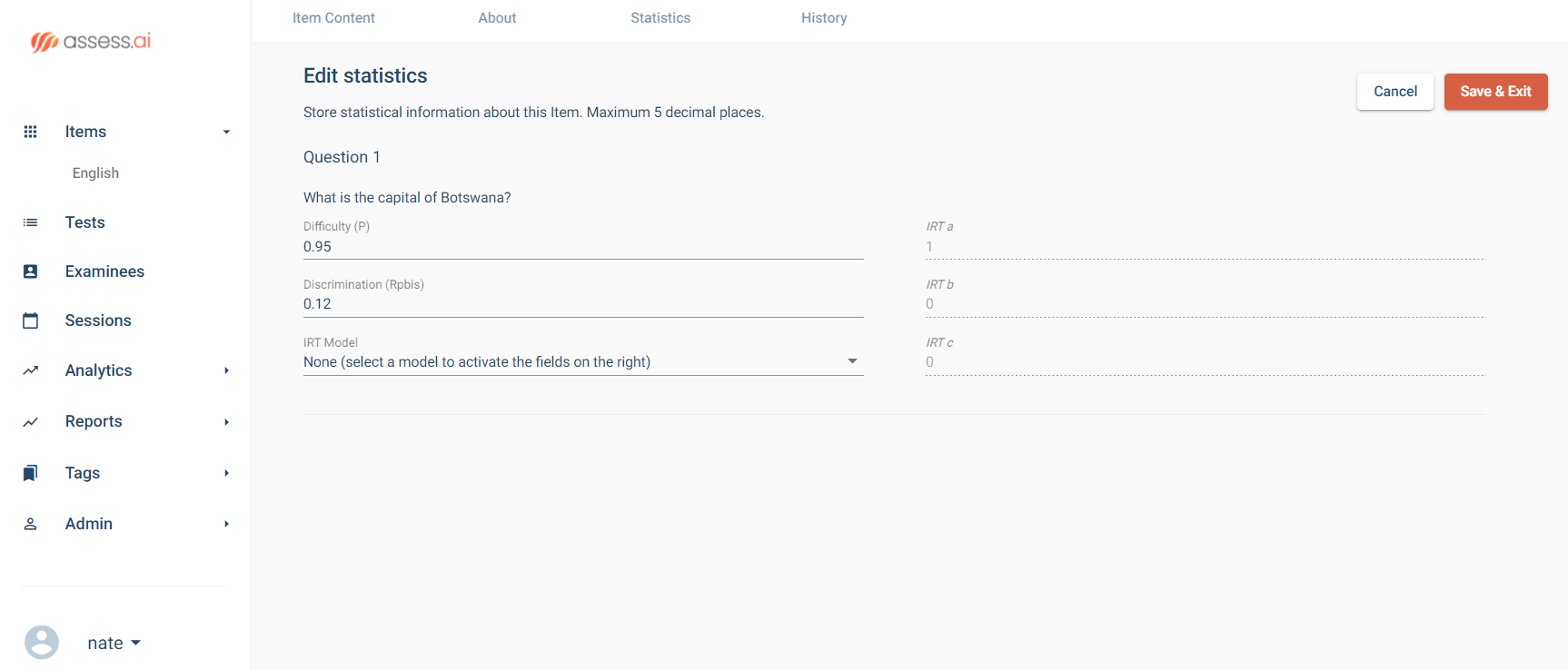
CTT quantifies item difficulty for dichotomous items as the proportion (P value) of examinees that correctly answer it.

It ranges from 0.0 to 1.0. A high value means that the item is easy, and a low value means that the item is difficult. There are no hard and fast rules because interpretation can vary widely for different situations. For example, a test given at the beginning of the school year would be expected to have low statistics since the students have not yet been taught the material. On the other hand, a professional certification exam, where someone can not even sit unless they have 3 years of experience and a relevant degree, might have all items appear easy even though they are quite advanced topics! Here are some general guidelines”

0.95-1.0 = Too easy (not doing much good to differentiate examinees, which is really the purpose of assessment)

0.60-0.95 = Typical

0.40-0.60 = Hard

<0.40 = Too hard (consider that a 4 option multiple choice has a 25% chance of pure guessing)

With Iteman, you can set bounds to automatically flag items. The minimum P value bound represents what you consider the cut point for an item being too difficult. For a relatively easy test, you might specify 0.50 as a minimum, which means that 50% of the examinees have answered the item correctly.

For a test where we expect examinees to perform poorly, the minimum might be lowered to 0.4 or even 0.3. The minimum should take into account the possibility of guessing; if the item is multiple-choice with four options, there is a 25% chance of randomly guessing the answer, so the minimum should probably not be 0.20. The maximum P value represents the cut point for what you consider to be an item that is too easy. The primary consideration here is that if an item is so easy that nearly everyone gets it correct, it is not providing much information about the examinees. In fact, items with a P of 0.95 or higher typically have very poor point-biserial correlations.

Note that because the scale is inverted (lower value means higher difficulty), this is sometimes referred to as item facility.

The Item Mean (Polytomous)

This refers to an item that is scored with 2 or more point levels, like an essay scored on a 0-4 point rubric or a Likert-type item that is “Rate on a scale of 1 to 5.”

1=Strongly Disagree
2=Disagree
3=Neutral
4=Agree
5=Strongly Agree

The item mean is the average of the item responses converted to numeric values across all examinees. The range of the item mean is dependent on the number of categories and whether the item responses begin at 0. The interpretation of the item mean depends on the type of item (rating scale or partial credit). A good rating scale item will have an item mean close to ½ of the maximum, as this means that on average, examinees are not endorsing categories near the extremes of the continuum.

You will have to adjust for your own situation, but here is an example for the 5-point Likert-style item.

1-2 is very low; people disagree fairly strongly on average

2-3 is low to neutral; people tend to disagree on average

3-4 is neutral to high; people tend to agree on average

4-5 is very high; people agree fairly strongly on average

Iteman also provides flagging bounds for this statistic. The minimum item mean bound represents what you consider the cut point for the item mean being too low. The maximum item mean bound represents what you consider the cut point for the item mean being too high.

The number of categories for the items must be considered when setting the bounds of the minimum/maximum values. This is important as all items of a certain type (e.g., 3-category) might be flagged.

Item Discrimination: Dichotomous

In psychometrics, discrimination is a GOOD THING, even though the word often has a negative connotation in general. The entire point of an exam is to discriminate amongst examinees; smart students should get a high score and not-so-smart students should get a low score. If everyone gets the same score, there is no discrimination and no point in the exam! Item discrimination evaluates this concept.

CTT uses the point-biserial item-total correlation (Rpbis) as its primary statistic for this.

The Pearson point-biserial correlation (r-pbis) is a measure of the discrimination or differentiating strength, of the item. It ranges from −1.0 to 1.0 and is a correlation of item scores and total raw scores. If you consider a scored data matrix (multiple-choice items converted to 0/1 data), this would be the correlation between the item column and a column that is the sum of all item columns for each row (a person’s score).

A good item is able to differentiate between examinees of high and low ability yet have a higher point-biserial, but rarely above 0.50. A negative point-biserial is indicative of a very poor item because it means that the high-ability examinees are answering incorrectly, while the low examinees are answering it correctly, which of course would be bizarre, and therefore typically indicates that the specified correct answer is actually wrong. A point-biserial of 0.0 provides no differentiation between low-scoring and high-scoring examinees, essentially random “noise.” Here are some general guidelines on interpretation. Note that these assume a decent sample size; if you only have a small number of examinees, many item statistics will be flagged!

0.20+ = Good item; smarter examinees tend to get the item correct

0.10-0.20 = OK item; but probably review it

0.0-0.10 = Marginal item quality; should probably be revised or replaced

<0.0 = Terrible item; replace it

***Major red flag is if the correct answer has a negative Rpbis and a distractor has a positive Rpbis

The minimum item-total correlation bound represents the lowest discrimination you are willing to accept. This is typically a small positive number, like 0.10 or 0.20. If your sample size is small, it could possibly be reduced. The maximum item-total correlation bound is almost always 1.0, because it is typically desired that the Rpbis be as high as possible.

The biserial correlation is also a measure of the discrimination or differentiating strength, of the item. It ranges from −1.0 to 1.0. The biserial correlation is computed between the item and total score as if the item was a continuous measure of the trait. Since the biserial is an estimate of Pearson’s r it will be larger in absolute magnitude than the corresponding point-biserial.

The biserial makes the stricter assumption that the score distribution is normal. The biserial correlation is not recommended for traits where the score distribution is known to be non-normal (e.g., pathology).

Item Discrimination: Polytomous

The Pearson’s r correlation is the product-moment correlation between the item responses (as numeric values) and total score. It ranges from −1.0 to 1.0. The r correlation indexes the linear relationship between item score and total score and assumes that the item responses for an item form a continuous variable. The r correlation and the Rpbis are equivalent for a 2-category item, so guidelines for interpretation remain unchanged.

The minimum item-total correlation bound represents the lowest discrimination you are willing to accept. Since the typical r correlation (0.5) will be larger than the typical Rpbis (0.3) correlation, you may wish to set the lower bound higher for a test with polytomous items (0.2 to 0.3). If your sample size is small, it could possibly be reduced. The maximum item-total correlation bound is almost always 1.0, because it is typically desired that the Rpbis be as high as possible.

The eta coefficient is an additional index of discrimination computed using an analysis of variance with the item response as the independent variable and total score as the dependent variable. The eta coefficient is the ratio of the between-groups sum of squares to the total sum of squares and has a range of 0 to 1. The eta coefficient does not assume that the item responses are continuous and also does not assume a linear relationship between the item response and total score.

As a result, the eta coefficient will always be equal or greater than Pearson’s r. Note that the biserial correlation will be reported if the item has only 2 categories.

Key and Distractor Analysis

In the case of many item types, it pays to evaluate the answers. A distractor is an incorrect option. We want to make sure that more examinees are not selecting a distractor than the key (P value) and also that no distractor has higher discrimination. The latter would mean that smart students are selecting the wrong answer, and not-so-smart students are selecting what is supposedly correct. In some cases, the item is just bad. In others, the answer is just incorrectly recorded, perhaps by a typo. We call this a miskey of the item. In both cases, we want to flag the item and then dig into the distractor statistics to figure out what is wrong.

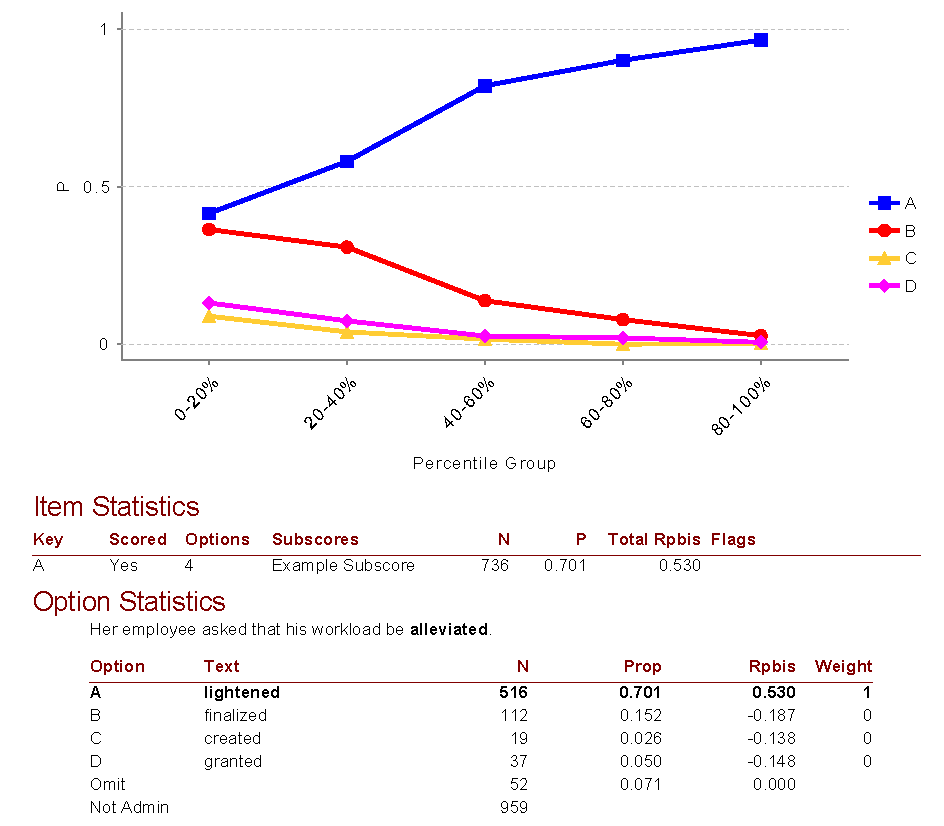
Example

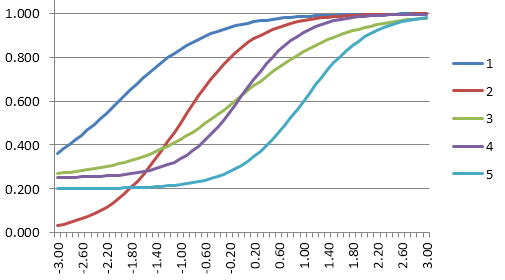
Here is an example output for one item from our Iteman software, which you can download for free. You might also be interested in this video. This is a very well-performing item. Here are some key takeaways.

This is a 4-option multiple choice item
It was on a subscore named “Example subscore”
This item was seen by 736 examinees
70% of students answered it correctly, so it was fairly easy, but not too easy
The Rpbis was 0.53 which is extremely high; the item is good quality
The line for the correct answer in the quantile plot has a clear positive slope, which reflects the high discrimination quality
The proportion of examinees selecting the wrong answers was nicely distributed, not too high, and with negative Rpbis values. This means the distractors are sufficiently incorrect and not confusing.

Item Analysis with Item Response Theory

Item Response Theory (IRT) is a very sophisticated paradigm of item analysis and tackles numerous psychometric tasks, from item analysis to equating to adaptive testing. It requires much larger sample sizes than CTT (100-1000 responses per item) and extensive expertise (typically a PhD psychometrician). Maximum Likelihood Estimation (MLE) is a key concept in IRT used to estimate model parameters for better accuracy in assessments.

IRT isn’t suitable for small-scale exams like classroom quizzes. However, it is used by virtually every “real” exam you will take in your life, from K-12 benchmark exams to university admissions to professional certifications.

If you haven’t used IRT, I recommend you check out this blog post first.

Item Difficulty

IRT evaluates item difficulty for dichotomous items as a b-parameter, which is sort of like a z-score for the item on the bell curve: 0.0 is average, 2.0 is hard, and -2.0 is easy. (This can differ somewhat with the Rasch approach, which rescales everything.) In the case of polytomous items, there is a b-parameter for each threshold, or step between points.

Item Discrimination

IRT evaluates item discrimination by the slope of its item response function, which is called the a-parameter. Often, values above 0.80 are good and below 0.80 are less effective.

Key and Distractor Analysis

In the case of polytomous items, the multiple b-parameters provide an evaluation of the different answers. For dichotomous items, the IRT modeling does not distinguish amongst correct answers. Therefore, we utilize the CTT approach for distractor analysis. This remains extremely important for diagnosing issues in multiple choice items.

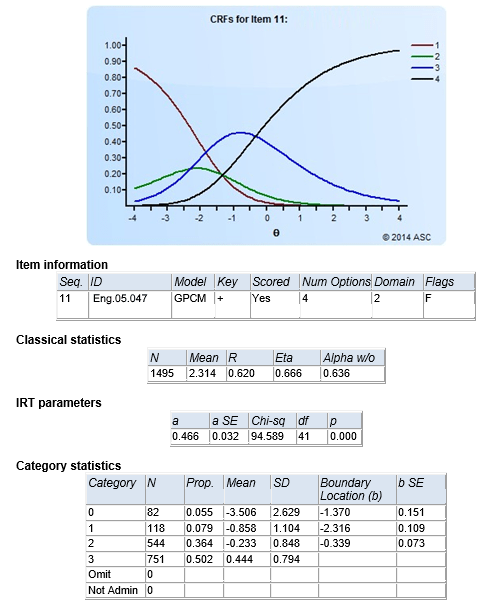
Example

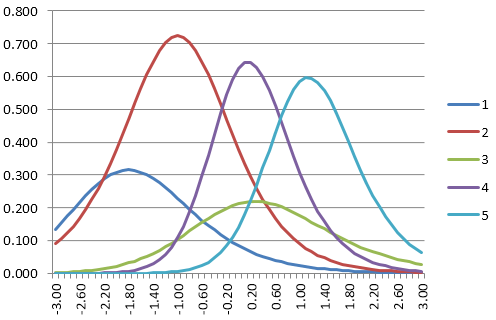
Here is an example of what output from an IRT analysis program (Xcalibre) looks like. You might also be interested in this video.

Here, we have a polytomous item, such as an essay scored from 0 to 3 points.
It is calibrated with the generalized partial credit model.
It has strong classical discrimination (0.62)
It has poor IRT discrimination (0.466)
The average raw score was 2.314 out of 3.0, so fairly easy
There was a sufficient distribution of responses over the four point levels
The boundary parameters are not in sequence; this item should be reviewed

Summary

This article is a very broad overview and does not do justice to the complexity of psychometrics and the art of diagnosing/revising items! I recommend that you download some of the item analysis software and start exploring your own data.

For additional reading, I recommend some of the common textbooks. For more on how to write/revise items, check out Haladyna (2004) and subsequent works. For item response theory, I highly recommend Embretson & Riese (2000).

March 31, 2021/by Nathan Thompson, PhD

Seven Technology Hacks to Deliver Assessments More Securely

Nathan Thompson, PhDMarch 27, 2021

So, yeah, the use of “hacks” in the title is definitely on the ironic and gratuitous side, but there is still a point to be made: are you making full use of current technology to keep your tests secure? Gone are the days when you are limited to linear test forms on paper in physical locations. Here are some quick points on how modern assessment technology can deliver assessments more securely, effectively, and efficiently than traditional methods:

1. AI delivery like CAT and LOFT

Psychometrics was one of the first areas to apply modern data science and machine learning (see this blog post for a story about a MOOC course). But did you know it was also one of the first areas to apply artificial intelligence (AI)? Early forms of computerized adaptive testing (CAT) were suggested in the 1960s and had become widely available in the 1980s. CAT delivers a unique test to each examinee by using complex algorithms to personalize the test. This makes it much more secure, and can also reduce test length by 50-90%.

2. Psychometric forensics

Modern psychometrics has suggested many methods for finding cheaters and other invalid test-taking behavior. These can range from very simple rules like flagging someone for having a top 5% score in a bottom 5% time, to extremely complex collusion indices. These approaches are designed explicitly to keep your test more secure.

3. Tech enhanced items

Tech enhanced items (TEIs) are test questions that leverage technology to be more complex than is possible on paper tests. Classic examples include drag and drop or hotspot items. These items are harder to memorize and therefore contribute to security.

4. IP address limits

Suppose you want to make sure that your test is only delivered in certain school buildings, campuses, or other geographic locations. You can build a test delivery platform that limits your tests to a range of IP addresses, which implements this geographic restriction.

5. Lockdown browser

A lockdown browser is a special software that locks a computer screen onto a test in progress, so for example a student cannot open Google in another tab and simply search for answers. Advanced versions can also scan the computer for software that is considered a threat, like a screen capture software.

6. Identity verification

Tests can be built to require unique login procedures, such as requiring a proctor to enter their employee ID and the test-taker to enter their student ID. Examinees can also be required to show photo ID, and of course, there are new biometric methods being developed.

7. Remote proctoring

The days are gone when you need to hop in the car and drive 3 hours to sit in a windowless room at a community college to take a test. Nowadays, proctors can watch you and your desktop via webcam. This is arguably as secure as in-person proctoring, and certainly more convenient and cost-effective.

So, how can I implement these to deliver assessments more securely?

Some of these approaches are provided by vendors specifically dedicated to that space, such as ProctorExam for remote proctoring. However, if you use ASC’s FastTest platform, all of these methods are available for you right out of the box. Want to see for yourself? Sign up for a free account!

March 27, 2021/by Nathan Thompson, PhD

IRT Test Information Function

Nathan Thompson, PhDFebruary 2, 2021

The IRT Test Information Function is a concept from item response theory (IRT) that is designed to evaluate how well an assessment differentiates examinees, and at what ranges of ability. For example, we might expect an exam composed of difficult items to do a great job in differentiating top examinees, but it is worthless for the lower half of examinees because they will be so confused and lost.

The reverse is true of an easy test; it doesn’t do any good for top examinees. The test information function quantifies this and has a lot of other important applications and interpretations.

IRT Test Information Function: how to calculate it

The test information function is not something you can calculate by hand. First, you need to estimate item-level IRT parameters, which define the item response function. The only way to do this is with specialized software; there are a few options in the market, but we recommend Xcalibre.

Next, the item response function is converted to an item information function for each item. The item information functions can then be summed into a test information function. Lastly, the test information function is often inverted into the conditional standard error of measurement function, which is extremely useful in test design and evaluation.

IRT Item Parameters

Software like Xcalibre will estimate a set of item parameters. The parameter you use depends on the item types and other aspects of your assessment.

For example, let’s just use the 3-parameter model, which estimates a, b, and c. And we’ll use a small test of 5 items. These are ordered by difficulty: item 1 is very easy and Item 5 is very hard.

Item	a	b	c
1	1.00	-2.00	0.20
2	0.70	-1.00	0.40
3	0.40	0.00	0.30
4	0.80	1.00	0.00
5	1.20	2.00	0.25

Item Response Function

The item response function uses the IRT equation to convert the parameters into a curve. The purpose of the item parameters is to fit this curve for each item, like a regression model to describe how it performs.

Here are the response functions for those 5 items. Note the scale on the x-axis, similar to the bell curve, with the easy items to the left and hard ones to the right.

Item Information Function

The item information function evaluates the calculus derivative of the item response function. An item provides more information about examinees where it provides more slope.

For example, consider Item 5: it is difficult, so it is not very useful for examinees in the bottom half of ability. The slope of the Item 5 IRF is then nearly 0 for that entire range. This then means that its information function is nearly 0.

Test Information Function

The test information function then sums up the item information functions to summarize where the test is providing information. If you imagine adding the graphs above, you can easily imagine some humps near the top and bottom of the range where there are the prominent IIFs.

Conditional Standard Error of Measurement Function

The test information function can be inverted into an estimate of the conditional standard error of measurement. What do we mean by conditional? If you are familiar with classical test theory, you know that it estimates the same standard error of measurement for everyone that takes a test.

But given the reasonable concepts above, it is incredibly unreasonable to expect this. If a test has only difficult items, then it measures top students well, and does not measure lower students well, so why should we say that their scores are just as accurate? The conditional standard error of measurement turns this into a function of ability.

Also, note that it refers to the theta scale and not to the number-correct scale.

How can I implement all this?

For starters, I recommend delving deeper into an item response theory book. My favorite is Item Response Theory for Psychologists by Embretson and Riese. Next, you need some item response theory software.

Xcalibre can be downloaded as a free version for learning and is the easiest program to learn how to use (no 1980s-style command code… how is that still a thing?). But if you are an R fan, there are plenty of resources in that community as well.

Tell me again: why are we doing this?

The purpose of all this is to effectively model how items and tests work, namely, how they interact with examinees. This then allows us to evaluate their performance so that we can improve them, thereby enhancing reliability and validity.

Classical test theory had a lot of shortcomings in this endeavor, which led to IRT being invented. IRT also facilitates some modern approaches to assessment, such as linear on-the-fly testing, adaptive testing, and multistage testing.

February 2, 2021/by Nathan Thompson, PhD

$math educational assessment$

What is Classical Item Difficulty (P Value)?

Nathan Thompson, PhDNovember 6, 2020

One of the core concepts in psychometrics is item difficulty. This refers to the probability that examinees will get the item correct for educational/cognitive assessments or respond in the keyed direction with psychological/survey assessments (more on that later). Difficulty is important for evaluating the characteristics of an item and whether it should continue to be part of the assessment; in many cases, items are deleted if they are too easy or too hard. It also allows us to better understand how the items and test as a whole operate as a measurement instrument, and what they can tell us about examinees.

I’ve heard of “item facility.” Is that similar?

Item difficulty is also called item facility, which is actually a more appropriate name. Why? The P value is a reverse of the concept: a low value indicates high difficulty, and vice versa. If we think of the concept as facility or easiness, then the P value aligns with the concept; a high value means high easiness. Of course, it’s hard to break with tradition, and almost everyone still calls it difficulty. But it might help you here to think of it as “easiness.”

How do we calculate classical item difficulty?

There are two predominant paradigms in psychometrics: classical test theory (CTT) and item response theory (IRT). Here, I will just focus on the simpler approach, CTT.

To calculate classical item difficulty with dichotomous items, you simply count the number of examinees that responded correctly (or in the keyed direction) and divide by the number of respondents. This gets you a proportion, which is like a percentage but is on the scale of 0 to 1 rather than 0 to 100. Therefore, the possible range that you will see reported is 0 to 1. Consider this data set.

Person	Item1	Item2	Item3	Item4	Item5	Item6	Score
1	0	0	0	0	0	1	1
2	0	0	0	0	1	1	2
3	0	0	0	1	1	1	3
4	0	0	1	1	1	1	4
5	0	1	1	1	1	1	5
Diff:	0.00	0.20	0.40	0.60	0.80	1.00

Item6 has a high difficulty index, meaning that it is very easy. Item4 and Item5 are typical items, where the majority of items are responding correctly. Item1 is extremely difficult; no one got it right!

For polytomous items (items with more than one point), classical item difficulty is the mean response value. That is, if we have a 5 point Likert item, and two people respond 4 and two response 5, then the average is 4.5. This, of course, is mathematically equivalent to the P value if the points are 0 and 1 for a no/yes item. An example of this situation is this data set:

Person	Item1	Item2	Item3	Item4	Item5	Item6	Score
1	1	1	2	3	4	5	1
2	1	2	2	4	4	5	2
3	1	2	3	4	4	5	3
4	1	2	3	4	4	5	4
5	1	2	3	5	4	5	5
Diff:	1.00	1.80	2.60	4.00	4.00	5.00

Note that this is approach to calculating difficulty is sample-dependent. If we had a different sample of people, the statistics could be quite different. This is one of the primary drawbacks to classical test theory. Item response theory tackles that issue with a different paradigm. It also has an index with the right “direction” – high values mean high difficulty with IRT.

If you are working with multiple choice items, remember that while you might have 4 or 5 responses, you are still scoring the items as right/wrong. Therefore, the data ends up being dichotomous 0/1.

Very important final note: this P value is NOT to be confused with p value from the world of hypothesis testing. They have the same name, but otherwise are completely unrelated. For this reason, some psychometricians call it P+ (pronounced “P-plus”), but that hasn’t caught on.

How do I interpret classical item difficulty?

For educational/cognitive assessments, difficulty refers to the probability that examinees will get the item correct. If more examinees get the item correct, it has low difficulty. For psychological/survey type data, difficulty refers to the probability of responding in the keyed direction. That is, if you are assessing Extraversion, and the item is “I like to go to parties” then you are evaluating how many examinees agreed with the statement.

What is unique with survey type data is that it often includes reverse-keying; the same assessment might also have an item that is “I prefer to spend time with books rather than people” and an examinee disagreeing with that statement counts as a point towards the total score.

For the stereotypical educational/knowledge assessment, with 4 or 5 option multiple choice items, we use general guidelines like this for interpretation.

Range	Interpretation	Notes
0.0-0.3	Extremely difficult	Examinees are at chance level or even below, so your item might be miskeyed or have other issues
0.3-0.5	Very difficult	Items in this range will challenge even top examinees, and therefore might elicit complaints, but are typically very strong
0.5-0.7	Moderately difficult	These items are fairly common, and a little on the tougher side
0.7-0.90	Moderately easy	These are the most common range of items on most classically built tests; easy enough that examinees rarely complain
0.90-1.0	Very easy	These items are mastered by most examinees; they are actually too easy to provide much info on examinees though, and can be detrimental to reliability.

Do I need to calculate this all myself?

No. There is plenty of software to do it for you. If you are new to psychometrics, I recommend CITAS, which is designed to get you up and running quickly but is too simple for advanced situations. If you have large samples or are involved with production-level work, you need Iteman. Sign up for a free account with the button below. If that is you, I also recommend that you look into learning IRT if you have not yet.

November 6, 2020/by Nathan Thompson, PhD

What can Machine Learning tell us about our item banks?

Nathan Thompson, PhDMarch 29, 2020

Artificial intelligence (AI) and machine learning (ML) have become buzzwords over the past few years. As I already wrote about, they are actually old news in the field of psychometrics. Factor analysis is a classical example of ML, and item response theory (IRT) also qualifies as ML. Computerized adaptive testing (CAT) is actually an application of AI to psychometrics that dates back to the 1970s.

One thing that is very different about the world of AI/ML today is the massive power available in free platforms like R, Python, and TensorFlow. I’ve been thinking a lot over the past few years about how these tools can impact the world of assessment. A straightforward application is too automated essay scoring; a common way to approach that problem is through natural language processing with the “bag of words” model and utilize the document-term matrix (DTM) as predictors in a model for essay score as a criterion variable. Surprisingly simple. This got me to wondering where else we could apply that sort of modeling. Obviously, student response data on selected-response items provides a ton of data, but the research questions are less clear. So, I turned to the topic that I think has the next largest set of data and text: item banks.

Step 1: Text Mining

The first step was to explore tools for text mining in R. I found this well-written and clear tutorial on the text2vec package and used that as my springboard. Within minutes I was able to get a document term matrix, and in a few more minutes was able to prune it. This DTM alone can provide useful info to an organization on their item bank, but I wanted to delve further. Can the DTM predict item quality?

Step 2: Fit Models

To do this, I utilized both the caret and glmnet packages to fit models. I love the caret package, but if you search the literature you’ll find it has a problem with sparse matrices, which is exactly what the DTM is. One blog post I found said that anyone with a sparse matrix is pretty much stuck using glmnet.

I tried a few models on a small item bank of 500 items from a friend of mine, and my adjusted R squared for the prediction of IRT parameters (as an index of item quality) was 0.53 – meaning that I could account for more than half the variance of item quality just by knowing some of the common words in each item’s stem. I wasn’t even using the answer texts n-grams, or additional information like Author and content domain.

Want to learn more about your item banks?

I’d love to swim even deeper on this issue. If you have a large item bank and would like to work with me to analyze it so you can provide better feedback and direction to your item writers and test developers, drop me a message at solutions@assess.com! This could directly impact the efficiency of your organization and the quality of your assessments.

March 29, 2020/by Nathan Thompson, PhD

Ways the Word “Standard” is used in Assessment

Nathan Thompson, PhDDecember 6, 2019

If you have worked in the field of assessment and psychometrics, you have undoubtedly encountered the word “standard.” While a relatively simple word, it has the potential to be confusing because it is used in three (and more!) completely different but very important ways. Here’s a brief discussion.

Standard = Cutscore

As noted by the well-known professor Gregory Cizek here, “standard setting refers to the process of establishing one or more cut scores on a test.” The various methods of setting a cutscore, like Angoff or Bookmark, are referred to as standard setting studies. In this context, the standard is the bar that separates a Pass from a Fail. We use methods like the ones mentioned to determine this bar in as scientific and defensible fashion as possible, and give it more concrete meaning than an arbitrarily selected round number like 70%. Selecting a round number like that will likely get you sued since there is no criterion-referenced interpretation.

Standard = Blueprint

If you work in the field of education, you often hear the term “educational standards.” These refer to the curriculum blueprints for an educational system, which also translate into assessment blueprints, because you want to assess what is on the curriculum. Several important ones in the USA are noted here, perhaps the most common of which nowadays is the Common Core State Standards, which attempted to standardize the standards across states. These standards exist to standardize the educational system, by teaching what a group of experts have agreed upon should be taught in 6th grade Math classes for example. Note that they don’t state how or when a topic should be taught, merely that 6th Grade Math should cover Number Lines, Measurement Scales, Variables, whatever – sometime in the year.

Standard = Guideline

If you work in the field of professional certification, you hear the term just as often but in a different context, accreditation standards. The two most common are the National Commission for Certifying Agencies (NCCA) and the ANSI National Accreditation Board (ANAB). These two organizations are a consortium of credentialing bodies that give a stamp of approval to credentialing bodies, stating that a Certification or Certificate program is legit. Why? Because there is no law to stop me from buying a textbook on any topic, writing 50 test questions in my basement, and selling it as a Certification. It is completely a situation of caveat emptor, and these organizations are helping the buyers by giving a stamp of approval that the certification was developed with accepted practices like a Job Analysis, Standard Setting Study, etc.

In addition, there are the professional standards for our field. These are guidelines on assessment in general rather than just credentialing. Two great examples are the AERA/APA/NCME Standards for Educational and Psychological Measurement and the International Test Commission’s Guidelines (yes they switch to that term) on various topics.

Also: Standardized = Equivalent Conditions

The word is also used quite frequently in the context of standardized testing, though it is rarely chopped to the root word “standard.” In this case, it refers to the fact that the test is given under equivalent conditions to provide greater fairness and validity. A standardized test does NOT mean multiple choice, bubble sheets, or any of the other pop connotations that are carried with it. It just means that we are standardizing the assessment and the administration process. Think of it as a scientific experiment; the basic premise of the scientific method is holding all variables constant except the variable in question, which in this case is the student’s ability. So we ensure that all students receive a psychometrically equivalent exam, with equivalent (as much as possible) writing utensils, scrap paper, computer, time limit, and all other practical surroundings. The problem comes with the lack of equivalence in access to study materials, prep coaching, education, and many bigger questions… but those are a societal issue and not a psychometric one.

So despite all the bashing that the term gets, a standardized test is MUCH better than the alternatives of no assessment at all, or an assessment that is not a level playing field and has low reliability. Consider the case of hiring employees: if assessments were not used to provide objective information on applicant skills and we could only use interviews (which are famously subjective and inaccurate), all hiring would be virtually random and the amount of incompetent people in jobs would increase a hundredfold. And don’t we already have enough people in jobs where they don’t belong?

December 6, 2019/by Nathan Thompson, PhD

Is teaching to the test a bad thing?

Nathan Thompson, PhDMarch 7, 2019

One of the most cliche phrases associated with assessment is “teaching to the test.” I’ve always hated this phrase, because it is only used in a derogatory matter, almost always by people who do not understand the basics of assessment and psychometrics. I recently saw it mentioned in this article on PISA, and that was one time too many, especially since it was used in an oblique, vague, and unreferenced manner.

So, I’m going to come out and say something very unpopular: in most cases, TEACHING TO THE TEST IS A GOOD THING.

Why teaching to the test is usually a good thing

If the test reflects the curriculum – which any good test will – then someone who is teaching to the test will be teaching to the curriculum. Which, of course, is the entire goal of teaching. The phrase “teaching to the test” is used in an insulting sense, especially because the alliteration is resounding and sellable, but it’s really not a bad thing in most cases. If a curriculum says that 4th graders should learn how to add and divide fractions, and the test evaluates this, what is the problem? Especially if it uses modern methodology like adaptive testing or tech-enhanced items to make the process more engaging and instructional, rather than oversimplifying to a text-only multiple choice question on paper bubble sheets?

The world of credentialing assessment, this is an extremely important link. Credential tests start with a job analysis study, which surveys professionals to determine what they consider to be the most important and frequently used skills in the job. This data is then transformed into test blueprints. Instructors for the profession, as well as aspiring students that are studying to pass the test, then focus on what is in the blueprints. This, of course, still contains the skills that are most important and frequently used in the job!

So what is the problem then?

Now, telling teachers how to teach is more concerning, and more likely to be a bad thing. Finland does well because it gives teachers lots of training and then power to choose how they teach, as noted in the PISA article.

As a counterexample, my high school math department made an edict starting my sophomore year that all teachers had to use the “Chicago Method.” It was pure bunk and based on the fact that students should be doing as much busy work as possible instead of the teachers actually teaching. I think it is because some salesman convinced the department head to make the switch so that they would buy a thousand brand new textbooks. The method makes some decent points (here’s an article from, coincidentally, when I was a sophomore in high school) but I think we ended up with a bastardization of it, as the edict was primarily:

Assign students to read the next chapter in class (instead of teaching them!); go sit at your desk.
Assign students to do at least 30 homework questions overnight, and come back tomorrow with any questions they have.
Answer any questions, then assign them the next chapter to read. Whatever you do, DO NOT teach them about the topic before they start doing the homework questions. Go sit at your desk.

Isn’t that preposterous? Unsurprisingly, after two years of this, I went from being a leader of the Math Team to someone who explicitly said “I am never taking Math again”. And indeed, I managed to avoid all math during my senior year of high school and first year of college. Thankfully, I had incredible professors in my years at Luther College, leading to me loving math again, earning a math major, and applying to grad school in psychometrics. This shows the effect that might happen with “telling teachers how to teach.” Or in this case, specifically – and bizarrely – to NOT teach.

What about all the bad tests out there?

Now, let’s get back to the assumption that a test does reflect a curriculum/blueprints. There are, most certainly, plenty of cases where an assessment is not designed or built well. That’s an entirely different problem, and is an entirely valid concern. I have seen a number of these in my career. This danger why we have international standards on assessments, like AERA/APA/NCME and NCCA. These provide guidelines on how a test should be build, sort of like how you need to build a house according to building code and not just throwing up some walls and a roof.

For example, there is nothing that is stopping me from identifying a career that has a lot of people looking to gain an edge over one another to get a better job… then buying a textbook, writing 50 questions in my basement, and throwing it up on a nice-looking website to sell as a professional certification. I might sell it for $395, and if I get just 100 people to sign up, I’ve made $39,500!!!! This violates just about every NCCA guideline, though. If I wanted to get a stamp of approval that my certification was legit – as well as making it legally defensible – I would need to follow the NCCA guidelines.

My point here is that there are definitely bad tests out there, just like there are millions of other bad products in the world. It’s a matter of caveat emptor. But just because you had some cheap furniture on college that broke right away, doesn’t mean you swear off on all furniture. You stay away from bad furniture.

There’s also the problem of tests being misused, but again that’s not a problem with the test itself. Certainly, someone making decisions is uninformed. It could actually be the best test in the world, with 100% precision, but if it is used for an invalid application then it’s still not a good situation. For example, if you took a very well-made exam for high school graduation and started using it for employment decisions with adults. Psychometricians call this validity – that we have evidence to support the intended use of the test and interpretations of scores. It is the #1 concern of assessment professionals, so if a test is being misused, it’s probably by someone without a background in assessment.

So where do we go from here?

Put it this way, if an overweight person is trying to become fitter, is success more likely to come from changing diet and exercise habits, or from complaining about their bathroom scale? Complaining unspecifically about a high school graduation assessment is not going to improve education; let’s change how we educate our children to prepare them for that assessment, and ensure that the assessment reflects the goals of the education. Nevertheless, of course, we need to invest in making the assessment as sound and fair as we can – which is exactly why I am in this career.

March 7, 2019/by Nathan Thompson, PhD

What is classical item facility?

Nathan Thompson, PhDOctober 28, 2018

Classical test theory is a century-old paradigm for psychometrics – using quantitative and scientific processes to develop and analyze assessments to improve their quality. (Nobody likes unfair tests!) The most basic and frequently used item statistic from classical test theory is the P-value. It is usually called item difficulty but is sometimes called item facility, which can lead to possible confusion.

The P-Value Statistic

The classical P-value is the proportion of examinees that respond correctly to a question, or respond in the “keyed direction” for items where the notion of correct is not relevant (imagine a personality assessment where all questions are Yes/No statements such as “I like to go to parties” … Yes is the keyed direction for an Extraversion scale). Note that this is NOT the same as the p-value that is used in hypothesis testing from general statistical methods. This P-value is almost universally agreed upon in terms of calculation. But some people call it item difficulty and others call it item facility. Why?

It has to do with the clarity interpretation. It usually makes sense to think of difficulty as an important aspect of the item. The P-value presents this, but in a reverse manner. We usually expect higher values to indicate more of something, right? But a P-value of 1.00 is high, and it means that there is not much difficulty; everyone gets the item correct, so it is actually no difficulty whatsoever. A P-value of 0.25 is low, but it means that there is a lot of difficulty; only 25% of examinees are getting it correct, so it has quite a lot of difficulty.

So where does “item facility” come in?

See how the meaning is reversed? It’s for this reason that some psychometricians prefer to call it item facility or item easiness. We still use the P-value, but 1.00 means high facility/easiness, and 0.25 means low facility/easiness. The direction of the semantics fits much better.

Nevertheless, this is a minority of psychometricians. There’s too much momentum to change an entire field at this point! It’s similar to the 3 dichotomous IRT parameters (a, b, c); some of you might have noticed that they are actually in the wrong order because the 1-parameter model does not use the parameter, it uses the b.

At the end of the day, it doesn’t really matter, but it’s another good example of how we all just got used to doing something and it’s now too far down the road to change it. Tradition is a funny thing.

October 28, 2018/by Nathan Thompson, PhD